题目内容
 如图,△ABD中∠BAD=90°,将△ABD逆时针旋转后得到△ACE,C点落在BD边上,∠E=25°,则∠BAC=
如图,△ABD中∠BAD=90°,将△ABD逆时针旋转后得到△ACE,C点落在BD边上,∠E=25°,则∠BAC=考点:旋转的性质
专题:计算题
分析:先根据旋转的性质得AB=AC,∠D=∠E=25°,再利用互余计算出∠B=90°-∠D=65°,接着根据等腰三角形的性质,由AB=AC得∠B=∠ACB=65°,然后根据三角形内角和求∠BAC的度数.
解答:解:∵△ABD逆时针旋转后得到△ACE,C点落在BD边上,
∴AB=AC,∠D=∠E=25°,
∵∠BAD=90°,
∴∠B=90°-∠D=65°,
∵AB=AC,
∴∠B=∠ACB=65°,
∴∠BAC=180°-∠B-∠ACB=50°.
故答案为50°.
∴AB=AC,∠D=∠E=25°,
∵∠BAD=90°,
∴∠B=90°-∠D=65°,
∵AB=AC,
∴∠B=∠ACB=65°,
∴∠BAC=180°-∠B-∠ACB=50°.
故答案为50°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图所示,C是线段AB的中点,D是线段AC的中点,已知线段AB长度是36,求线段DB的长度.
如图所示,C是线段AB的中点,D是线段AC的中点,已知线段AB长度是36,求线段DB的长度.
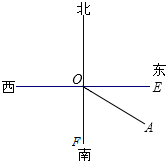 如图,货轮D在航行过程中,发现灯塔A在它的南偏东60°的方向上.同时,在货轮D的北偏西30°、西北方向上又发现了客轮B和海岛C.
如图,货轮D在航行过程中,发现灯塔A在它的南偏东60°的方向上.同时,在货轮D的北偏西30°、西北方向上又发现了客轮B和海岛C.