题目内容
1.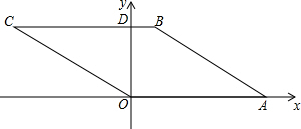 如图,在直角坐标系中,菱形OABC的边OA在x的正半轴上,其面积为18,顶点O的坐标为(0,0),顶点A的坐标为(6,0),顶点B在第一象限,边BC与x轴相交于点D,点E在边OA上,将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA,则△OEF的面积为( )
如图,在直角坐标系中,菱形OABC的边OA在x的正半轴上,其面积为18,顶点O的坐标为(0,0),顶点A的坐标为(6,0),顶点B在第一象限,边BC与x轴相交于点D,点E在边OA上,将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA,则△OEF的面积为( )| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
分析 根据点A的坐标求出OA=6,再根据面积求出OD=3,根据翻折变换的性质以及周角等于360°求出∠DEF=135°,再求出∠DEO=45°,从而判断出△ODE是等腰直角三角形,∠OEF=90°,然后求出OE,再求出AE即EF的长,即可求出△OEF的面积.
解答 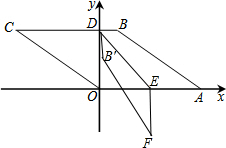 解:如图所示:
解:如图所示:
∵点A(6,0),
∴OA=6,
∵菱形OABC的面积为18,
∴OD•OA=6•OD=18,
解得OD=3,
∵四边形ABDE沿直线DE翻折,FE⊥EA,
∴∠DEF=$\frac{1}{2}$(360°-90°)=135°,
∴∠DEO=135°-90°=45°,∠OEF=90°,
∴△ODE是等腰直角三角形,
∴OE=OD=3,
∴EF=AE=6-3=3,
∴△OEF的面积为$\frac{1}{2}$×3×3=$\frac{9}{2}$;
故选:D.
点评 本题考查了菱形的性质、坐标与图形性质以及翻折变换的性质;熟记性质并判断出△ODE是等腰直角三角形是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
11.计算1-5等于( )
| A. | 6 | B. | 4 | C. | -4 | D. | -6 |
16.一元二次方程x2+4x+4=0的根是( )
| A. | x1=4,x2=-4 | B. | x1=x2=-2 | C. | x1=2,x2=-2 | D. | x1=0,x2=-2 |
 如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=2时,四边形ABEC是矩形.
如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=2时,四边形ABEC是矩形.