题目内容
6.先化简,再求值:$\frac{x+2}{x+1}$-$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$+($\frac{x}{x-1}$-$\frac{x}{{x}^{2}-1}$).其中x是不等式组$\left\{\begin{array}{l}{2x-1<5}\\{x+7>1}\end{array}\right.$的整数解.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,求出不等式组的解集确定出x的值,代入计算即可求出值.
解答 解:原式=$\frac{x+2}{x+1}$-$\frac{x(x-1)}{(x-1)^{2}}$÷$\frac{{x}^{2}+x-x}{(x+1)(x-1)}$=$\frac{x+2}{x+1}$-$\frac{x}{x-1}$•$\frac{(x+1)(x-1)}{{x}^{2}}$=$\frac{x+2}{x+1}$-$\frac{x+1}{x}$=$\frac{{x}^{2}+2x-{x}^{2}-2x-1}{x(x+1)}$=-$\frac{1}{x(x+1)}$,
由不等式组$\left\{\begin{array}{l}{2x-1<5}\\{x+7>1}\end{array}\right.$,解得:-6<x<3,
当x=2时,原式=-$\frac{1}{6}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.点M(-2,3)在曲线y=$\frac{k}{x}$上,则下列点一定在该曲线上的是( )
| A. | (2,3) | B. | (-2,-3) | C. | (3,-2) | D. | (3,2) |
14.为了防控H7N9禽流感,某校积极进行校园环境消毒,为此购买了甲、乙两种消毒液,已知购买过的两次这两种消毒液的甁数和总费用如表所示
(1)求甲种消毒液和乙种消毒液每瓶的售价;
(2)销售员提示,现在买乙种消毒液有优惠,具体方法是:如果买乙种消毒液超过30瓶,那么超出部分可以享受七五折优惠,学校现规定,从甲、乙两消毒液中买其中一种消毒液,数量为100瓶,请你帮助学校判断一下买哪种消毒液比较省钱,并说明理由.
| 甲种消毒液(瓶) | 乙种消毒液(瓶) | 总费用(元) | |
| 第一次 | 30 | 50 | 740 |
| 第二次 | 40 | 45 | 770 |
(2)销售员提示,现在买乙种消毒液有优惠,具体方法是:如果买乙种消毒液超过30瓶,那么超出部分可以享受七五折优惠,学校现规定,从甲、乙两消毒液中买其中一种消毒液,数量为100瓶,请你帮助学校判断一下买哪种消毒液比较省钱,并说明理由.
1.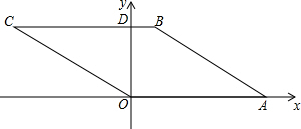 如图,在直角坐标系中,菱形OABC的边OA在x的正半轴上,其面积为18,顶点O的坐标为(0,0),顶点A的坐标为(6,0),顶点B在第一象限,边BC与x轴相交于点D,点E在边OA上,将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA,则△OEF的面积为( )
如图,在直角坐标系中,菱形OABC的边OA在x的正半轴上,其面积为18,顶点O的坐标为(0,0),顶点A的坐标为(6,0),顶点B在第一象限,边BC与x轴相交于点D,点E在边OA上,将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA,则△OEF的面积为( )
 如图,在直角坐标系中,菱形OABC的边OA在x的正半轴上,其面积为18,顶点O的坐标为(0,0),顶点A的坐标为(6,0),顶点B在第一象限,边BC与x轴相交于点D,点E在边OA上,将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA,则△OEF的面积为( )
如图,在直角坐标系中,菱形OABC的边OA在x的正半轴上,其面积为18,顶点O的坐标为(0,0),顶点A的坐标为(6,0),顶点B在第一象限,边BC与x轴相交于点D,点E在边OA上,将四边形ABDE沿直线DE翻折,使点A落在第四象限的点F处,且FE⊥EA,则△OEF的面积为( )| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
11.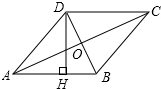 如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为( )
如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为( )
 如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为( )
如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为( )| A. | 5cm | B. | 10cm | C. | $\frac{24}{5}$cm | D. | $\frac{48}{5}$cm |
15.某生物兴趣小组在恒温箱中培养两种菌种,甲种菌种生长的温度在34℃~37℃之间,乙种菌种生长的温度是35℃~38℃之间,那么恒温箱的温度t℃应该设定的范围是( )
| A. | 34℃~38℃ | B. | 35℃~37℃ | C. | 34℃~35℃ | D. | 37℃~38℃ |
 如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD、CE相交于点O,求证:BO=2OD.
如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD、CE相交于点O,求证:BO=2OD.