题目内容
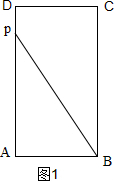
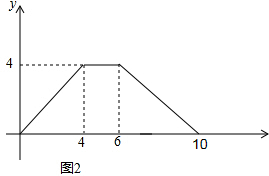
已知:如图1,长方形ABCD中,AB=2,动点P在长方形的边BC,CD,DA上沿B→C→D→A的方向运动,且点P与点B,A都不重合.图2是此运动过程中,△ABP的面积y与点P经过的路程x之间的函数图象的一部分.
请结合以上信息回答下列问题:
(1)长方形ABCD中,边BC的长为 ;
(2)若长方形ABCD中,M为CD边的中点,当点P运动到与点M重合时,x= ,y= ;
(3)当6≤x≤10时,y与x之间的函数关系式是 ;
(4)利用第(3)问求得的结论,在图2中将相应的y与x的函数图象补充完整.

请结合以上信息回答下列问题:
(1)长方形ABCD中,边BC的长为
(2)若长方形ABCD中,M为CD边的中点,当点P运动到与点M重合时,x=
(3)当6≤x≤10时,y与x之间的函数关系式是
(4)利用第(3)问求得的结论,在图2中将相应的y与x的函数图象补充完整.

考点:四边形综合题,动点问题的函数图象
专题:
分析:(1)由图象2看出当点P到达点C时,即x=4时,△ABP的面积最大,根据面积公式求出BC;
(2)由长方形ABCD的边长AB=2,BC=4,可求出x=BC+
AB,此时△ABP的面积是4,可从图象上看也可计算;
(3)当6≤x≤10时,求出AP,再根据三角形的面积公式求出y与x之间的函数关系式;
(4)根据6≤x≤10时,y与x之间的函数关系式补全图象.
(2)由长方形ABCD的边长AB=2,BC=4,可求出x=BC+
| 1 |
| 2 |
(3)当6≤x≤10时,求出AP,再根据三角形的面积公式求出y与x之间的函数关系式;
(4)根据6≤x≤10时,y与x之间的函数关系式补全图象.
解答:解:(1)∵当点P到达点C时,△ABP的面积最大,
∴△ABP的面积=
×AB×BC=4
∵AB=2,
∴BC=4,
故答案为:4.
(2)∵M为CD边的中点,AB=2,BC=4,
∴x=4+1=5,此时的y=
AB•BC=4,
故答案为:5,4.
(3)如图,当6≤x≤10时,
∵AP=4-(t-6)=10-t,
∴△ABP的面积=
AB•AP=10-t,
∴y与x之间的函数关系式是:y=10-t.
故答案为:y=10-t.
(4)如图2,利用6≤x≤10时,y与x之间的函数关系式是:y=10-t补全图象.
∴△ABP的面积=
| 1 |
| 2 |
∵AB=2,
∴BC=4,
故答案为:4.
(2)∵M为CD边的中点,AB=2,BC=4,
∴x=4+1=5,此时的y=
| 1 |
| 2 |
故答案为:5,4.
(3)如图,当6≤x≤10时,

∵AP=4-(t-6)=10-t,
∴△ABP的面积=
| 1 |
| 2 |
∴y与x之间的函数关系式是:y=10-t.
故答案为:y=10-t.
(4)如图2,利用6≤x≤10时,y与x之间的函数关系式是:y=10-t补全图象.

点评:本题主要考查了四边形综合题及动点问题的函数图象.解题的关键是根据点P不同的位置得出y与x之间的函数关系式.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
下列命题中,真命题是( )
| A、对角线互相平分的四边形是菱形 |
| B、对角线互相垂直的四边形是菱形 |
| C、对角线相等的平行四边形是菱形 |
| D、对角线平分一组对角的平行四边形是菱形 |
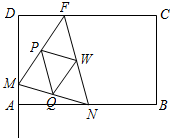 如图,矩形ABCD的边AB=6cm,BC=4cm,点F在DC上,DF=2cm.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,再连接△FMN三边的中点得
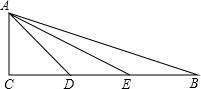
如图,矩形ABCD的边AB=6cm,BC=4cm,点F在DC上,DF=2cm.动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,再连接△FMN三边的中点得 如图,在△ABC中,AB=AC,AC的垂直平分线DE交BC于D,连结AD,∠B=50°.求∠ADC的度数.
如图,在△ABC中,AB=AC,AC的垂直平分线DE交BC于D,连结AD,∠B=50°.求∠ADC的度数.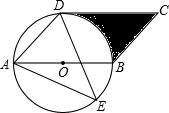 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,若⊙O的半径为6cm,且∠AED=45°.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,若⊙O的半径为6cm,且∠AED=45°.