题目内容
如图，在△ABC中，DE∥BC，AD=3DB，△ABC的面积为72．求：△ADE的面积、四边形DEBC的面积．考点：相似三角形的判定与性质
专题：
分析：由已知条件可证得△ADE∽△ABC，则由相似三角形的面积之比等于相似比的平方．
解答：解：∵AD=3DB，
∴
=
．
∵DE∥BC，
∴△ADE∽△ABC．
∴
=(
)2，即
=
，
解得 S△ADE=4.5，
则S四边形DBCE=S△ABC-S△ADE=72-4.5=67.5．
解：∵AD=3DB，∴
| AD |
| AB |
| 1 |
| 4 |
∵DE∥BC，
∴△ADE∽△ABC．
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
| S△ADE |
| 72 |
| 1 |
| 16 |
解得 S△ADE=4.5，
则S四边形DBCE=S△ABC-S△ADE=72-4.5=67.5．
点评：本题考查了相似三角形的判定和性质，相似三角形的面积之比等于相似比的平方．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
化简
-
的结果是（ ）
| a2 |
| a-b |
| b2 |
| a-b |
| A、a+b |
| B、a-b |
| C、a2+b2 |
| D、1 |
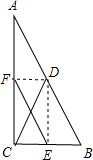如图，△ABC中，∠ACB=90°，CD是AB上的中线，EF是中位线，下列说法不正确的是（ ）| A、四边形CEDF是矩形 |
| B、CD与EF互相平分 |
| C、CE=CF |
| D、CD=EF |
如图，在△ABC中，AB=AC，AC的垂直平分线DE交BC于D，连结AD，∠B=50°．求∠ADC的度数．