题目内容
4．在同一个圆中，甲、乙、丙、丁四个扇形的面积之比为1：2：3：4，分别求出这四个扇形圆心角的度数．分析 根据扇形的面积比，求出各个扇形的圆心角之比，从而求出各个扇形的圆心角占整个圆的几分之几，进而确定出各个扇形的圆心角．
解答 解：∵甲、乙、丙、丁四个扇形的面积之比为1：2：3：4，
∴各个扇形的面积分别占整个圆面积的$\frac{1}{10}$，$\frac{1}{5}$，$\frac{3}{10}$，$\frac{2}{5}$，
∴各个扇形的圆心角的度数分别360°×$\frac{1}{10}$=36°，360°×$\frac{1}{5}$=72°，360°×$\frac{3}{10}$=108°，360°×$\frac{2}{5}$=144°，
答：甲、乙、丙、丁四个扇形的圆心角的度数分别是36°，72°，108°，144°．
点评 本题考查了扇形统计图，关键是根据四个扇形的面积之比求出它们所占的圆心角的度数之比．
练习册系列答案
相关题目
如图，在直角坐标系中，△ABC的顶点坐标分别为A（-6，0），B（2，0），C（-1，8），求△ABC的面积．
9．
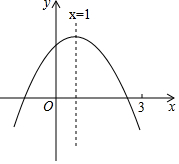二次函数y=ax2+bx+c（a≠0）图象如图，下列结论正确的是（ ）
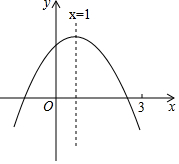二次函数y=ax2+bx+c（a≠0）图象如图，下列结论正确的是（ ）| A． | abc＞0 | |
| B． | 若ax12+bx1=ax22+bx2且x1≠x2，则x1+x2=1 | |
| C． | a-b+c＞0 | |
| D． | 当m≠1时，a+b＞am2+bm |
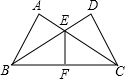如图，已知∠A=∠D=90°，AB=DC，AC与BD相交于E，F是BC的中点，求证：∠BEF=∠CEF．
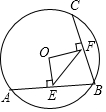如图，在半径为5的⊙O中，弦AB=8，点C是优弧$\widehat{AB}$上一点（不与A、B重合），OE⊥AB于E，OF⊥BC于F，求cos∠EFB的值．