题目内容
14.明明与亮亮玩摸球游戏,在一个袋子中放有7个完全一样的球,分别标有1、2、3、4、5、6、7七个数字,明明与亮亮轮流坐庄,从袋中摸出一球,记下号码,然后放回,规定:如果摸到的球号码大于4,则明明胜,否则亮亮胜.你认为这个游戏公平吗?请说明理由.若不公平如何修改游戏规则使明明和亮亮游戏公平?分析 根据概率公式分别求出两人获胜的概率,比较大小即可得出答案.
解答 解:从分别标有1、2、3、4、5、6、7七个数字的7个球中摸出一个球有7种等可能结果,
其中数字大于4的有3种,不大于4的有4种,
∴P(明明)=$\frac{3}{7}$,P(亮亮)=$\frac{4}{7}$,
又∵$\frac{3}{7}$≠$\frac{4}{7}$,
∴不公平;
修改规则:如果摸到的球号码大于4,则明明胜,如果摸到的球号码小于4,则亮亮胜.(符合题意即可).
点评 本题主要考查游戏的公平性,熟练掌握概率公式是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.已知三角形的每条边长是整数,且小于等于4,这样的互不全等的三角形有( )
| A. | 10个 | B. | 12个 | C. | 13个 | D. | 14 |
2. 已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
①∠PAD=∠PDA=60°;
②△PAO≌△ADE;
③PO=$\sqrt{2}$r;
④AO:OP:PA=1:$\sqrt{2}$:$\sqrt{3}$.
 已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )①∠PAD=∠PDA=60°;
②△PAO≌△ADE;
③PO=$\sqrt{2}$r;
④AO:OP:PA=1:$\sqrt{2}$:$\sqrt{3}$.
| A. | ①④ | B. | ②③ | C. | ③④ | D. | ①③④ |
9.下列各命题都成立,其中逆命题也成立的是( )
| A. | 若a>0,b>0,则a+b>0 | B. | 对顶角相等 | ||
| C. | 全等三角形的对应角相等 | D. | 平行四边形的两组对边分别相等 |
19.已知关于x的方程(m-1)x2+x+1=0有一个根,则m的值是( )
| A. | $\frac{5}{4}$ | B. | 1 | C. | $-\frac{5}{4}$ | D. | 1或$\frac{5}{4}$ |
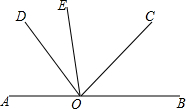 如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.
如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.