题目内容
15.解方程(1)5x-7=9-3x
(2)$\frac{1-2x}{3}$=$\frac{3x+1}{7}$-3.
分析 (1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)方程5x-7=9-3x,
移项,得:5x+3x=9+7,
合并同类项,得:8x=16,
系数化为1,得:x=2;
(2)方程$\frac{1-2x}{3}$=$\frac{3x+1}{7}$-3,
去分母,得:7(1-2x)=3(3x+1)-3×3×7,
去括号,得:7-14x=9x+3-63,
移项,得:-14x-9 x=3-63-7,
合并同类项,得:-23x=-67,
系数化为1,得:x=$\frac{67}{23}$.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.如果3xm+2y3与-2x3y2n-1是同类项,则m、n的值分别是( )
| A. | m=1,n=2 | B. | m=0,n=2 | C. | m=2,n=1 | D. | m=1,n=1 |
20.若点P(2m-1,3m+1)在第二象限,则m的取值范围是( )
| A. | m>$\frac{1}{2}$ | B. | m$<-\frac{1}{3}$ | C. | $-\frac{1}{3}<m<\frac{1}{2}$ | D. | -3<m<$\frac{1}{2}$ |
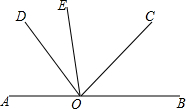 如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.
如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.