Question

14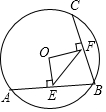．如图，在半径为5的⊙O中，弦AB=8，点C是优弧$\widehat{AB}$上一点（不与A、B重合），OE⊥AB于E，OF⊥BC于F，求cos∠EFB的值．

Answer 1

分析 连接AC，作直径BH，连接AH，根据垂径定理和三角形中位线定理得到EF∥AC，根据勾股定理求出AH，根据余弦的定义计算即可．

解答 解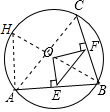：连接AC，作直径BH，连接AH，
∵OE⊥AB于E，OF⊥BC于F，
∴BF=FC，BE=EA，
∴EF∥AC，
∴∠EFB=∠C，
∵BH为直径，
∴∠HAB=90°，
∴AH=$\sqrt{B{H}^{2}-A{B}^{2}}$=6，
∴cos∠H=$\frac{HA}{BH}$=$\frac{6}{10}$=$\frac{3}{5}$，
∴cos∠EFB=$\frac{3}{5}$．

点评 本题考查的是垂直定理、圆周角定理、三角形的中位线定理，掌握垂直弦的直径平分这条弦，并且平分弦所对的两条弧是解题的关键．