题目内容
6.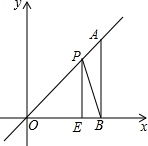 如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )| A. | 4+2$\sqrt{2}$ | B. | 4+$\sqrt{10}$ | C. | 6 | D. | 4$\sqrt{2}$ |
分析 在y轴的正半轴上截取OF=OE=3,连接EF,证得F是E关于直线y=x的对称点,连接BF交OA于P,此时△BEP周长最小,最小值为BF+EB,根据勾股定理求得BF,因为BE=1,所以△BEP周长最小值为BF+EB=5+1=6.
解答  解:在y轴的正半轴上截取OF=OE=3,连接EF,
解:在y轴的正半轴上截取OF=OE=3,连接EF,
∵A点为直线y=x上一点,
∴OA垂直平分EF,
∴E、F是直线y=x的对称点,
连接BF交OA于P,根据两点之间线段最短可知此时△BEP周长最小,最小值为BF+EB;
∵OF=3,OB=4,
∴BF=$\sqrt{O{F}^{2}+O{B}^{2}}$=5,
∵EB=4-3=1,
△BEP周长最小值为BF+EB=5+1=6.
故选C.
点评 本题考查了轴对称的判定和性质,轴对称-最短路线问题,勾股定理的应用等,作出P点是解题的关键.

练习册系列答案
相关题目
16.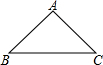 如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )
如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )
 如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )
如图,已知△ABC中,AB=AC=5,BC=8.则cosB的值是( )| A. | 1.25 | B. | 0.8 | C. | 0.6 | D. | 0.625 |
 如图所示,在山脚C处测得山顶A仰角为30°,沿着水平地面向前300米到达点D,在D点测得山顶A的仰角为60°,求AB.
如图所示,在山脚C处测得山顶A仰角为30°,沿着水平地面向前300米到达点D,在D点测得山顶A的仰角为60°,求AB.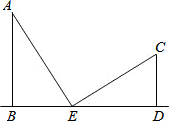 如图,两根电线杆AB,CD垂直于地面,AB=5cm,CD=3cm,现在施工人员在两根电线杆的底端之间(线段BD上)选一点E分别向电线杆顶端A,C拉钢索AE,CE,如果正好测得∠AEC=90°,且AE=CE.那么BE的长为多少?
如图,两根电线杆AB,CD垂直于地面,AB=5cm,CD=3cm,现在施工人员在两根电线杆的底端之间(线段BD上)选一点E分别向电线杆顶端A,C拉钢索AE,CE,如果正好测得∠AEC=90°,且AE=CE.那么BE的长为多少?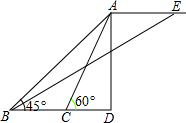 如图,广场上空有一个气球A,地面上点B、C、D在一条直线上,BC=20m,两个观测者在点B、C两处分别测得气球A的仰角∠ABD=45°,∠ACD=60°,当气球沿与BC的平行的路线飘移10秒后至达点E,在B处测得气球的仰角为30°.
如图,广场上空有一个气球A,地面上点B、C、D在一条直线上,BC=20m,两个观测者在点B、C两处分别测得气球A的仰角∠ABD=45°,∠ACD=60°,当气球沿与BC的平行的路线飘移10秒后至达点E,在B处测得气球的仰角为30°.