题目内容
11.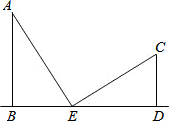 如图,两根电线杆AB,CD垂直于地面,AB=5cm,CD=3cm,现在施工人员在两根电线杆的底端之间(线段BD上)选一点E分别向电线杆顶端A,C拉钢索AE,CE,如果正好测得∠AEC=90°,且AE=CE.那么BE的长为多少?
如图,两根电线杆AB,CD垂直于地面,AB=5cm,CD=3cm,现在施工人员在两根电线杆的底端之间(线段BD上)选一点E分别向电线杆顶端A,C拉钢索AE,CE,如果正好测得∠AEC=90°,且AE=CE.那么BE的长为多少?
分析 利用全等三角形的判定方法得出△ABE≌△EDC(AAS),进而求出BE的长.
解答 解:∵∠AEC=90°,
∴∠AEB+∠CED=90°,
∵∠CED+∠C=90°,
∴∠C=∠AEB,
在△ABE和△EDC中,
$\left\{\begin{array}{l}{∠ABE=∠EDC}\\{∠BEA=∠C}\\{AE=EC}\end{array}\right.$,
∴△ABE≌△EDC(AAS),
∴BE=DC=3m.
答:BE的长为3m.
点评 此题主要考查了全等三角形的应用,根据题意得出△ABE≌△EDC是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.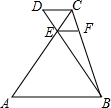 如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )
如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )
 如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )
如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
19. 如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )
如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )
 如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )
如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )| A. | 40° | B. | 45° | C. | 73° | D. | 85° |
6.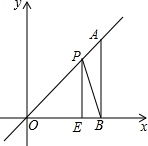 如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
 如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )| A. | 4+2$\sqrt{2}$ | B. | 4+$\sqrt{10}$ | C. | 6 | D. | 4$\sqrt{2}$ |
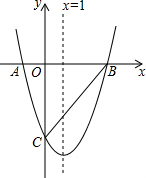 如图,对称轴为x=1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(-1,0).
如图,对称轴为x=1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(-1,0).