题目内容
15.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为2cm,则其腰上的高为$\sqrt{3}$cm.分析 本题要分情况讨论.当等腰三角形的顶角是钝角或者等腰三角形的顶角是锐角两种情况,在等腰三角形腰上的高与另一腰构建的直角三角形中,已知了30°的特殊角,通过解直角三角形即可求出高的长度.
解答  解:①当为锐角三角形时,如图1,
解:①当为锐角三角形时,如图1,
在Rt△ABD中,∠ABD=30°,AB=2cm,
所以,BD=AB•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$(cm);
②当为钝角三角形时,如图2,
在Rt△ACD中,∠ACD=30°,AC=2cm,
所以,CD=AC•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$(cm);
故答案为:$\sqrt{3}$.
点评 本题主要考查了等腰三角形的性质以及解直角三角形的应用.准确画出图形利用数形结合是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
6.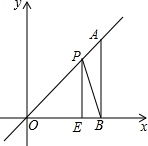 如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
 如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )| A. | 4+2$\sqrt{2}$ | B. | 4+$\sqrt{10}$ | C. | 6 | D. | 4$\sqrt{2}$ |
