题目内容
6.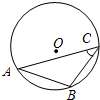 如图,点C是⊙O上的动点,弦AB=4,∠C=45°,则S△ABC的最大值是( )
如图,点C是⊙O上的动点,弦AB=4,∠C=45°,则S△ABC的最大值是( )| A. | $2\sqrt{2}$+4 | B. | 8 | C. | $2\sqrt{3}$+4 | D. | 4$\sqrt{2}$+4 |
分析 过点O作OE⊥AB于点E,OE的反向延长线交⊙O于点D,连接OA,OB,根据圆周角定理求出∠AOB=90°,由勾股定理求出OA的长,根据垂径定理求出AE的长,进而可得出OE的长,根据三角形的面积公式即可得出结论.
解答  解:过点O作OE⊥AB于点E,OE的反向延长线交⊙O于点D,连接OA,OB,
解:过点O作OE⊥AB于点E,OE的反向延长线交⊙O于点D,连接OA,OB,
∵AB是定值,
∴DE越长,则△ABC的面积越大.
∵∠C=45°,
∴∠AOB=90°,
∴△OAB是等腰直角三角形,
∴OA=2$\sqrt{2}$.
∵OE⊥AB,
∴AE=2,
∴OE=$\sqrt{{OA}^{2}-{AE}^{2}}$=$\sqrt{{(2\sqrt{2})}^{2}-{2}^{2}}$=2,
∴DE=2$\sqrt{2}$+2,
∴当点C于点D重合时,△ABC的面积最大,即S△ABC=$\frac{1}{2}$AB•DE=$\frac{1}{2}$×4×(2$\sqrt{2}$+2)=4$\sqrt{2}$+4.
故选D.
点评 本题考查的是圆周角定理,根据题意画出图形,构造出圆周角是解答此题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
7.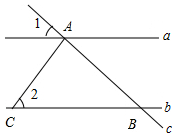 如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
 如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )| A. | 38° | B. | 42° | C. | 48° | D. | 58° |
18. 如图,O为?ABCD对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形有( )
如图,O为?ABCD对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形有( )
 如图,O为?ABCD对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形有( )
如图,O为?ABCD对角线AC,BD的交点,EF经过点O,且与边AD,BC分别交于点E,F,则图中的全等三角形有( )| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |
15. 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠2=25°,则∠1的度数为( )
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠2=25°,则∠1的度数为( )
 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠2=25°,则∠1的度数为( )
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠2=25°,则∠1的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
16.据统计,2015年长沙市的常住人口约为7500000人,将数据7500000用科学记数法表示为( )
| A. | 7.5×106 | B. | 0.75×107 | C. | 7.5×107 | D. | 75×105 |
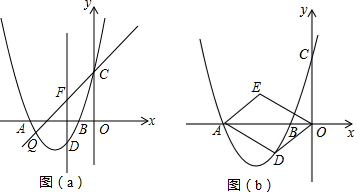
 当某一面积S关于某一线段x是一次函数时,则称S是关于x的奇特面积.如图,∠BAC=45°,点D在AC边上,且DA=2.点P,Q同时从D点出发,分别沿射线DC、射线DA运动,P点的运行速度是Q点的$\sqrt{2}$倍,当点Q到达A时,点P,Q同时停止运动.过点Q作AC的垂线段QR,使QR=PQ,连接PR.设QD=x,△PQR和∠BAC重叠部分的面积为S,请问S是否存在关于x的奇特面积?若存在,求奇特面积S关于x的函数关系式;若不存在,请说明理由.
当某一面积S关于某一线段x是一次函数时,则称S是关于x的奇特面积.如图,∠BAC=45°,点D在AC边上,且DA=2.点P,Q同时从D点出发,分别沿射线DC、射线DA运动,P点的运行速度是Q点的$\sqrt{2}$倍,当点Q到达A时,点P,Q同时停止运动.过点Q作AC的垂线段QR,使QR=PQ,连接PR.设QD=x,△PQR和∠BAC重叠部分的面积为S,请问S是否存在关于x的奇特面积?若存在,求奇特面积S关于x的函数关系式;若不存在,请说明理由. 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=4,则GH的长为$\frac{4}{3}$.
如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=4,则GH的长为$\frac{4}{3}$.