题目内容
11. 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=4,则GH的长为$\frac{4}{3}$.
如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=4,则GH的长为$\frac{4}{3}$.
分析 根据平行线分线段成比例定理得出$\frac{GH}{AB}=\frac{CH}{BC}$,$\frac{GH}{CD}=\frac{BH}{BC}$,将两个式子相加,即可求出GH的长.
解答 解:∵AB∥CH∥CD,
∴$\frac{GH}{AB}=\frac{CH}{BC}$,$\frac{GH}{CD}=\frac{BH}{BC}$,
∴$\frac{GH}{AB}$+$\frac{GH}{CD}$=$\frac{CH}{BC}$+$\frac{BH}{BC}$=1,
∵AB=2,CD=4,
∴$\frac{GH}{2}$+$\frac{GH}{4}$=1,
解得:GH=$\frac{4}{3}$;
故答案为:$\frac{4}{3}$.
点评 本题考查了平行线分线段成比例定理;由平行线分线段成比例定理得出比例式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若方程3x2-4x-4=0的两个实数根分别为x1,x2,则x1+x2=( )
| A. | -4 | B. | 3 | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
19.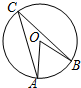 如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )
如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )
 如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )
如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )| A. | 60° | B. | 50° | C. | 45° | D. | 30° |
6.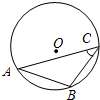 如图,点C是⊙O上的动点,弦AB=4,∠C=45°,则S△ABC的最大值是( )
如图,点C是⊙O上的动点,弦AB=4,∠C=45°,则S△ABC的最大值是( )
 如图,点C是⊙O上的动点,弦AB=4,∠C=45°,则S△ABC的最大值是( )
如图,点C是⊙O上的动点,弦AB=4,∠C=45°,则S△ABC的最大值是( )| A. | $2\sqrt{2}$+4 | B. | 8 | C. | $2\sqrt{3}$+4 | D. | 4$\sqrt{2}$+4 |
1.长沙市中考体育分值已经提高到了60分,其中的必考项目就有男子引体向上和女子一分钟仰卧起坐,各校为此加强了对体育训练的重视.
引体向上(男)和一分钟仰卧起坐(女)共16分 单位:次数
注:0.5次是指考生从直臂悬垂开始,有正确的引体动作和下杠动作,但未完整完成一次
某中学对全校学生这两项运动的成绩进行了统计,规定分值15分及以上为优秀,12分到14分为良好,6分到10分为合格,6分以下不合格,在全校800名初三学生中,随机抽取部分学生进行测试,并将测试成绩绘制成如下两幅不完整的统计图,求:
(1)某女生说她得了12分,请问她一分钟做了多少次仰卧起坐;
(2)请问一共抽取了多少名学生?并补全条形统计图;
(3)根据抽样结果估计,本校项目由多少学生能够得优秀?

引体向上(男)和一分钟仰卧起坐(女)共16分 单位:次数
| 分值 | 16 | 15 | 14 | 13 | 12 | 10 | 8 | 6 | 3 | |
| 成绩 | 男(次) | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0.5 |
| 女(次) | 45 | 40 | 36 | 32 | 28 | 25 | 22 | 20 | <19 | |
某中学对全校学生这两项运动的成绩进行了统计,规定分值15分及以上为优秀,12分到14分为良好,6分到10分为合格,6分以下不合格,在全校800名初三学生中,随机抽取部分学生进行测试,并将测试成绩绘制成如下两幅不完整的统计图,求:
(1)某女生说她得了12分,请问她一分钟做了多少次仰卧起坐;
(2)请问一共抽取了多少名学生?并补全条形统计图;
(3)根据抽样结果估计,本校项目由多少学生能够得优秀?

