题目内容
15．
如图，直线l∥m，将含有45°角的三角板ABC的直角顶点C放在直线m上，若∠2=25°，则∠1的度数为（ ）| A． | 20° | B． | 25° | C． | 30° | D． | 35° |
分析 先根据对顶角的定义得出∠3的度数，再由三角形内角和定理求出∠4的度数，根据平行线的性质求出∠ACD的度数，进而可得出结论．
解答 
解：∵∠2=25°，
∴∠3=∠2=25°．
∵∠A=45°，
∴∠4=180°-45°-25°=110°．
∵直线l∥m，
∴∠ACD=110°，
∴∠1=110°-90°=20°．
故选A．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等是解答此题的关键．
练习册系列答案
相关题目
5．统计学校排球队员的年龄，发现有12、13、14、15等四种年龄，统计结果如下表：
根据表中信息可以判断该排球队员的平均年龄为（ ）
| 年龄（岁） | 12 | 13 | 14 | 15 |
| 人数（个） | 2 | 4 | 6 | 8 |
| A． | 13 | B． | 14 | C． | 13.5 | D． | 5 |
6．
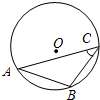如图，点C是⊙O上的动点，弦AB=4，∠C=45°，则S△ABC的最大值是（ ）
如图，点C是⊙O上的动点，弦AB=4，∠C=45°，则S△ABC的最大值是（ ）| A． | $2\sqrt{2}$+4 | B． | 8 | C． | $2\sqrt{3}$+4 | D． | 4$\sqrt{2}$+4 |
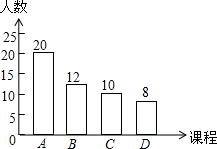某中学计划开设A、B、C、D四门校本课程供学生选修，规定每个学生必须并且只能选修其中一门，为了了解学生的选修意向，现随机抽取了部分学生进行调查，并将调查结果绘制成如图所示的条形统计图，已知该校学生人数为1200人，由此可以估计选修B课程的学生约有288人．
4．
如图，直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A（2，m）、B（-6，n）两点．则当y1＜y2时，x的取值范围是（ ）
如图，直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A（2，m）、B（-6，n）两点．则当y1＜y2时，x的取值范围是（ ）| A． | x＞-6或0＜x＜2 | B． | -6＜x＜0或x＞2 | C． | x＜-6或0＜x＜2 | D． | -6＜x＜2 |
