��Ŀ����
1�� ��ijһ���S����ijһ�߶�x��һ�κ���ʱ�����S�ǹ���x�������������ͼ����BAC=45�㣬��D��AC���ϣ���DA=2����P��Qͬʱ��D��������ֱ�������DC������DA�˶���P��������ٶ���Q���$\sqrt{2}$��������Q����Aʱ����P��Qͬʱֹͣ�˶�������Q��AC�Ĵ��߶�QR��ʹQR=PQ������PR����QD=x����PQR�͡�BAC�ص����ֵ����ΪS������S�Ƿ���ڹ���x����������������ڣ����������S����x�ĺ�����ϵʽ���������ڣ���˵�����ɣ�
��ijһ���S����ijһ�߶�x��һ�κ���ʱ�����S�ǹ���x�������������ͼ����BAC=45�㣬��D��AC���ϣ���DA=2����P��Qͬʱ��D��������ֱ�������DC������DA�˶���P��������ٶ���Q���$\sqrt{2}$��������Q����Aʱ����P��Qͬʱֹͣ�˶�������Q��AC�Ĵ��߶�QR��ʹQR=PQ������PR����QD=x����PQR�͡�BAC�ص����ֵ����ΪS������S�Ƿ���ڹ���x����������������ڣ����������S����x�ĺ�����ϵʽ���������ڣ���˵�����ɣ�
���� �������������S��x�ĺ�����ϵʽ���ٸ���S�ǹ���x��������������жϼ��ɽ�����⣮
��� �⣺���ڣ��������£�
����R��AB��ʱ���ߡ�A=45�㣬RQ��AC��
��AQ=RQ=PQ��
��2-x=x+$\sqrt{2}$x��
��x=2-$\sqrt{2}$��
�ٵ�0��x$��2-\sqrt{2}$ʱ��ͼ1�У�S=$\frac{1}{2}$PQ2=$\frac{1}{2}$��3+2$\sqrt{2}$��x2��
�ڵ�2-$\sqrt{2}$��x��2ʱ����ͼ2�У�
��RQ��AC��RQ=PQ��
���R=��RPQ=45�㣬
�ߡ�A=45�㣬
���A+��RPQ=90�㣬
���AFP=90��=��EFR��
��RE=RQ-EQ=��1+$\sqrt{2}$��x-��2-x����
��S=S��PQR-S��EFR=$\frac{1}{2}$��3+2$\sqrt{2}$��2-$\frac{1}{4}$[��1+$\sqrt{2}$��x-��2-x��]2=��2+$\sqrt{2}$��x-1��
������������2-$\sqrt{2}$��x��2��S=��2+$\sqrt{2}$��x-1��һ�κ�����
�൱2-$\sqrt{2}$��x��2��S�ǹ���x�����������
���� ���⿼��һ�κ����ۺ��⡢����ֱ�������ε����ʡ������������֪ʶ������Ĺؼ����������⣬ѧ������������S��x�ĺ�����ϵ�������п�ѹ���⣮

��ϰ��ϵ�д�
 ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д�
�����Ŀ
2�� ��ͼ��ֱ��l1��l2��CD��AB�ڵ�D����1=50�㣬���BCD�Ķ���Ϊ��������
��ͼ��ֱ��l1��l2��CD��AB�ڵ�D����1=50�㣬���BCD�Ķ���Ϊ��������
 ��ͼ��ֱ��l1��l2��CD��AB�ڵ�D����1=50�㣬���BCD�Ķ���Ϊ��������
��ͼ��ֱ��l1��l2��CD��AB�ڵ�D����1=50�㣬���BCD�Ķ���Ϊ��������| A�� | 50�� | B�� | 45�� | C�� | 40�� | D�� | 30�� |
9��һԪ���η���x2-2x+3=0�ĸ�������ǣ�������
| A�� | ����������ȵ�ʵ���� | B�� | ��������ȵ�ʵ���� | ||
| C�� | ��һ��ʵ���� | D�� | û��ʵ���� |
6��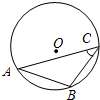 ��ͼ����C�ǡ�O�ϵĶ��㣬��AB=4����C=45�㣬��S��ABC�����ֵ�ǣ�������
��ͼ����C�ǡ�O�ϵĶ��㣬��AB=4����C=45�㣬��S��ABC�����ֵ�ǣ�������
 ��ͼ����C�ǡ�O�ϵĶ��㣬��AB=4����C=45�㣬��S��ABC�����ֵ�ǣ�������
��ͼ����C�ǡ�O�ϵĶ��㣬��AB=4����C=45�㣬��S��ABC�����ֵ�ǣ�������| A�� | $2\sqrt{2}$+4 | B�� | 8 | C�� | $2\sqrt{3}$+4 | D�� | 4$\sqrt{2}$+4 |
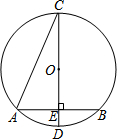 ��ͼ���ڡ�O�У�CD��ֱ������AB��CD������ΪE������C=15�㣬AB=6cm�����O�뾶Ϊ6cm��
��ͼ���ڡ�O�У�CD��ֱ������AB��CD������ΪE������C=15�㣬AB=6cm�����O�뾶Ϊ6cm��
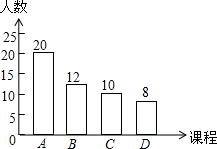 ij��ѧ�ƻ�����A��B��C��D����У���γ̹�ѧ��ѡ�ޣ��涨ÿ��ѧ�����벢��ֻ��ѡ������һ�ţ�Ϊ���˽�ѧ����ѡ�������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ��ʾ������ͳ��ͼ����֪��Уѧ������Ϊ1200�ˣ��ɴ˿��Թ���ѡ��B�γ̵�ѧ��Լ��288�ˣ�
ij��ѧ�ƻ�����A��B��C��D����У���γ̹�ѧ��ѡ�ޣ��涨ÿ��ѧ�����벢��ֻ��ѡ������һ�ţ�Ϊ���˽�ѧ����ѡ�������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ��ʾ������ͳ��ͼ����֪��Уѧ������Ϊ1200�ˣ��ɴ˿��Թ���ѡ��B�γ̵�ѧ��Լ��288�ˣ� ��ͼ����ƽ���ı���ABCD�У���EΪAD���е㣬�ӳ�CE��BA���ӳ����ڵ�F��
��ͼ����ƽ���ı���ABCD�У���EΪAD���е㣬�ӳ�CE��BA���ӳ����ڵ�F��