题目内容
14.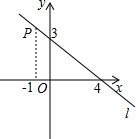 如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;
如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;(1)直线l的截距为3;
(2)点P的坐标为(-1,$\frac{15}{4}$),直线l上所有位于点P朝上一侧的点的横坐标的取值范围是x<-1,这些点的坐标的取值范围是y>$\frac{15}{4}$;
(3)如果直线l的表达式为y=kx+b,那么关于x的不等式kx+b>0的解集是x<4,kx+b<0的解集是x>4.
分析 (1)根据直线的截距的定义求解;
(2)先利用待定系数法求出直线l的解析式,再计算自变量为-1的函数值即可得到P点坐标,然后观察函数图象求解;
(3)利用直线l与x轴的交点为(4,0),然后利用函数图象可得到不等式kx+b>0和kx+b<0的解集.
解答 解:(1)直线l的截距为3;
(2)设直线l的解析式为y=kx+b,
把(4,0),(0,3)代入得$\left\{\begin{array}{l}{4k+b=0}\\{b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$,
所以直线l的解析式为y=-$\frac{3}{4}$x+3,
当x=-1时,y=-$\frac{3}{4}$x+3=$\frac{15}{4}$,则点P的坐标为(-1,$\frac{15}{4}$),直线l上所有位于点P朝上一侧的点的横坐标的取值范围是x<-1,这些点的纵坐标的取值范围是y>$\frac{15}{4}$;
(3)当x<4时,y>0,即不等式kx+b>0的解集是x<4,
当x>4时,y<0,即kx+b<0的解集是x>4.
故答案为3;(-1,$\frac{15}{4}$),x<-1,y>$\frac{15}{4}$;x<4,x>4.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
2.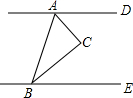 若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
 若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
5.已知抛物线y=ax2-2ax+m与x轴相交于A(-1,0)、B两点,与y轴负半轴相交于点C,且S△ABC=6,则( )
| A. | 在y轴右侧该抛物线上不存在点M,使S△ACM=3 | |
| B. | 在y轴右侧该抛物线上存在两个点M,使S△ACM=3 | |
| C. | 在y轴右侧该抛物线上存在唯一的点M(2,3),使S△ACM=3 | |
| D. | 在y轴右侧该抛物线上存在唯一的点M(2,-3),使S△ACM=3 |
6.下列数值中,是不等式x≥-2的解的是( )
| A. | -1 | B. | -3 | C. | -5 | D. | -9 |
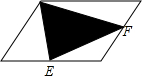 已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积.
已知平行四边形的面积是128平方厘米,E、F分别是两条边上的中点,求阴影部分的面积.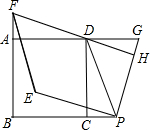 如图已知,四边形ABCD是正方形,点P与点G分别在线段BC与线段AD的延长线上,PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.
如图已知,四边形ABCD是正方形,点P与点G分别在线段BC与线段AD的延长线上,PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.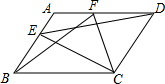 如图,在平行四边形ABCD中,点E是AB边上一点,点F是AD边上一点,试说明S△ECD=S△FBC的理由.
如图,在平行四边形ABCD中,点E是AB边上一点,点F是AD边上一点,试说明S△ECD=S△FBC的理由. 已知?ABCD中,AE平分∠BAD交BC于点E,且BE=3,EC=2,求?ABCD的周长.
已知?ABCD中,AE平分∠BAD交BC于点E,且BE=3,EC=2,求?ABCD的周长.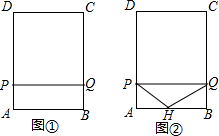 如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).
如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).