题目内容
9.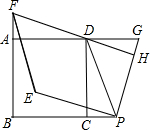 如图已知,四边形ABCD是正方形,点P与点G分别在线段BC与线段AD的延长线上,PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.
如图已知,四边形ABCD是正方形,点P与点G分别在线段BC与线段AD的延长线上,PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连接EF.求证:四边形PEFD是菱形.
分析 作PM⊥AG垂足为M,先证明四边形DCPM是矩形,再证明△ADF≌△MPG得DF=PG=PD=PE,由DF∥PE,DF=PD,得到四边形PEFD是平行四边形,再由PE=PD得出结论.
解答 证明: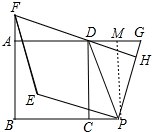 作PM⊥AG垂足为M,
作PM⊥AG垂足为M,
∵DH⊥GP,
∴∠PMG=∠DHG=90°,
∵∠MPG+∠G=90°,∠G+∠HDG=90°
∴∠HDG=∠MPG,
∵∠ADF=∠HDH,
∴∠ADF=MPG,
∵四边形ABCD是正方形,
∴AD=DC=AB=BC,∠BAD=∠ADC=∠BCD=90°,
∴∠MDC=∠PMD=∠DCP=90°,
∴四边形DCPM是矩形,
∴CD=PM,
在△ADF和△MPG中,
$\left\{\begin{array}{l}{∠FAD=∠PMG}\\{AD=PM}\\{∠ADF=∠MPG}\end{array}\right.$,
∴△ADF≌△MPG,
∴DF=PG=PE,
∵EP⊥PG,FH⊥PG,
∴FH∥PE,
∵DF=PE,DF∥PE,
∴四边形PEFD是平行四边形,
∵PD=PG=PE,
∴四边形PEFD是菱形.
点评 本题考查菱形的判定、全等三角形的判定和性质、平行四边形的性质等知识,解题的关键是添加辅助线构造全等三角形,属于中考常考题型.

练习册系列答案
相关题目
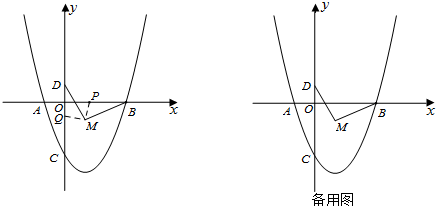
17.如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),交y轴于C点,其部分值对应如下表:
(1)求该二次函数的解析式;
(2)⊙M过A、B、C三点,交y轴于另一点D,求圆心M和D点的坐标;
(3)连接BM、DM,将∠BMD绕点M逆时针旋转,两边BM、DM与x轴、y轴分别交于P、Q.若△PBM为等腰三角形,求Q点的坐标.
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | -3 | -3 |
(2)⊙M过A、B、C三点,交y轴于另一点D,求圆心M和D点的坐标;
(3)连接BM、DM,将∠BMD绕点M逆时针旋转,两边BM、DM与x轴、y轴分别交于P、Q.若△PBM为等腰三角形,求Q点的坐标.

19.若不等式(a-1)x≤-3的解集为x≥$\frac{3}{1-a}$,则a的取值范围是( )
| A. | a>1 | B. | a<1 | C. | a>0 | D. | a≤1 |
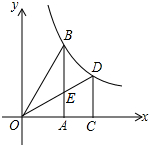 y=$\frac{3\sqrt{2}}{x}$.
y=$\frac{3\sqrt{2}}{x}$.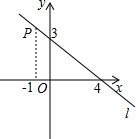 如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;
如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;