题目内容
4. 一列快车从甲地驶往乙地,一辆慢车从乙地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究:
一列快车从甲地驶往乙地,一辆慢车从乙地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究:(1)甲、乙两地的距离为1200km,点D表示慢车到达甲地;
(2)求慢车和快车的速度;
(3)求a,b的值.
分析 (1)根据坐标系中A点纵坐标为1200,得出甲乙两地距离即可;根据两车相距1200km,则点D即是慢车到达甲地;
(2)根据图中D点坐标即可得出慢车速度,进而利用B点坐标得出快车速度;
(3)根据速度和时间即可求出C点坐标.
解答 解:(1)∵图中的折线表示y与x之间的函数关系,
∴坐标系中A点纵坐标即为两地距离,即1200km,图中点D的纵坐标为1200,则D点的实际意义是:慢车到达甲地;
(2)由图得出慢车整个的过程行驶时了1200km,行驶时间为15h,
∴慢车的速度为:1200÷15=80(km/h),
∵6小时两车相遇,
∴慢车行驶距离为:6×80=480(km),
∴快车行驶了:1200-480=720(km),
∴快车的速度为:720÷6=120(km/h);
(3)∵快车的速度为:120km/h,
∴行驶剩余的路程需要:480÷120=4(h),
此时两车一共行驶了(120+80)×4=800(km),
∴C点坐标为:(10,800),
∴a=10,b=800.
点评 此题主要考查了一次函数的应用,利用图表中数据得出慢车速度是解题关键.

练习册系列答案
相关题目
14.二次函数y=-x2+bx+c的图象的最高点是(-1,-3),则b,c的值分别是( )
| A. | 2,4 | B. | 2,-4 | C. | -2,4 | D. | -2,-4 |
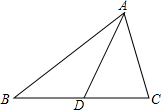 如图,AD为△ABC中BC边上的中线,试说明S△ABD=S△ADC.
如图,AD为△ABC中BC边上的中线,试说明S△ABD=S△ADC.