题目内容
14.已知a,b,c为△ABC的三边,且满足a2+b2+c2+50=10a+6b+8c,试判断△ABC的形状,并说明理由.分析 把已知的式子变形,利用完全平方公式分组因式分解,出现三个非负数的平方和等于0的形式,求出a、b、c的数值,再进一步探讨得出答案即可.
解答 解:由a2+b2+c2+50=10a+6b+8c,
得:(a2-10a+25)+(b2-6b+9)+(c2-8c+16)=0,
即:(a-5)2+(b-3)2+(c-4)2=0,
a-5=0,b-3=0,c-4=0
解得a=5,b=3,c=4,
∵32+42=25=52,即a2=b2+c2,
∴∠A=90°,
即三角形ABC为直角三角形.
点评 本题考查勾股定理的逆定理的应用、完全平方公式、非负数的性质.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.下列语句错误的是( )
| A. | $\frac{1}{4}$的平方根是±$\frac{1}{2}$ | B. | -$\frac{1}{4}$的平方根是-$\frac{1}{2}$ | ||
| C. | $\frac{1}{4}$的算术平方根是$\frac{1}{2}$ | D. | $\frac{1}{4}$有两个平方根,它们互为相反数 |
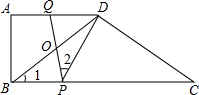 如图,在四边形ABCD中,AD∥BC,∠A=90°,BD=DC,AB=6,AD=8,点P、Q分别为BC、AD上的动点,连接PQ,与BD相交于点O,
如图,在四边形ABCD中,AD∥BC,∠A=90°,BD=DC,AB=6,AD=8,点P、Q分别为BC、AD上的动点,连接PQ,与BD相交于点O,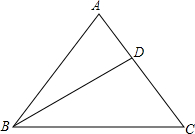 如图,△ABC中,∠ABC=∠C,点D是AC边上一点,∠A=∠ADB,∠DBC=30°,求∠BDC的度数.
如图,△ABC中,∠ABC=∠C,点D是AC边上一点,∠A=∠ADB,∠DBC=30°,求∠BDC的度数. 一列快车从甲地驶往乙地,一辆慢车从乙地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究:
一列快车从甲地驶往乙地,一辆慢车从乙地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究: