题目内容
14.二次函数y=-x2+bx+c的图象的最高点是(-1,-3),则b,c的值分别是( )| A. | 2,4 | B. | 2,-4 | C. | -2,4 | D. | -2,-4 |
分析 根据二次函数y=-x2+bx+c的二次项系数-1来确定该函数的图象的开口方向,由二次函数y=-x2+bx+c的图象的最高点是(-1,-3)确定该函数的顶点坐标,然后根据顶点坐标公式解答b、c的值.
解答 解:∵二次函数y=-x2+bx+c的二次项系数-1<0,
∴该函数的图象的开口方向向下,
∴二次函数y=-x2+bx+c的图象的最高点坐标(-1,-3)就是该函数的顶点坐标,
∴-1=$\frac{b}{2}$,即b=-2;①
-3=$\frac{-4c-{b}^{2}}{-4}$,即b2+4c+12=0;②
由①②解得,b=-2,c=-4;
故选:D.
点评 本题考查对二次函数最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一列快车从甲地驶往乙地,一辆慢车从乙地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究:
一列快车从甲地驶往乙地,一辆慢车从乙地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行以下探究: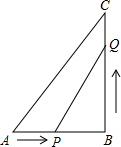 在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,P从A开始出发向点B以2cm/s的速度移动,同时点Q从点B开始出发向C以沿1cm/s的速度移动,一个点到达终点后,另一个点也随之停止移动,设运动的时间为x秒.
在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,P从A开始出发向点B以2cm/s的速度移动,同时点Q从点B开始出发向C以沿1cm/s的速度移动,一个点到达终点后,另一个点也随之停止移动,设运动的时间为x秒.