题目内容
13．
如图，a∥b，∠1=∠2，∠3=40°，则∠4等于70°．
分析 先根据平行线的性质求出∠1+∠2的度数，由∠1=∠2可得出∠2的度数，进而可得出结论．
解答 解：∵a∥b，∠3=40°，
∴∠1+∠2=180°-40°=140°，∠2=∠4，
∵∠1=∠2，
∴∠2=70°，
∴∠4=∠2=70°．
故答案为：70°．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．
练习册系列答案
快捷英语周周练系列答案
相关题目
3．
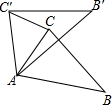如图，在△ABC中，∠CAB=75°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（ ）
如图，在△ABC中，∠CAB=75°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 75° |
4．下列各数中是无理数的是（ ）
| A． | $\frac{10}{3}$ | B． | 3.1415 | C． | $\root{3}{8}$ | D． | $\sqrt{2}$ |
1．将点A（3，2）沿x轴向左平移4个单位长度，再沿y轴向下平移4个单位长度后得到点A′，则点A′的坐标是（ ）
| A． | （1，2） | B． | （1，-2） | C． | （-1，2） | D． | （-1，-2） |
8．将抛物线y=x2-2x+3向上平移2个单位长度，再向左平移3个单位长度后，得到的抛物线的解析式为（ ）
| A． | y=（x+2）2+4 | B． | y=（x-4）2+4 | C． | y=（x+2）2 | D． | y=（x-4）2+6 |
18．
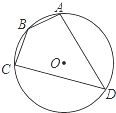如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠B=135°，则弧AC的长（ ）
如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠B=135°，则弧AC的长（ ）| A． | 2π | B． | π | C． | $\frac{π}{2}$ | D． | 4π |
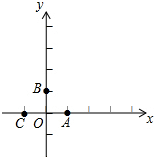如图，在平面直角坐标系中，点A，B，C的坐标分别为（1，0），（0，1），（-1，0）．一个电动玩具从坐标原点0出发，第一次跳跃到点P1．使得点P1与点O关于点A成中心对称；第二次跳跃到点P2，使得点P2与点P1关于点B成中心对称；第三次跳跃到点P3，使得点P3与点P2关于点C成中心对称；第四次跳跃到点P4，使得点P4与点P3关于点A成中心对称；第五次跳跃到点P5，使得点P5与点P4关于点B成中心对称；…照此规律重复下去，则点P7的坐标是（2，0），点P2016的坐标为（0，0）．
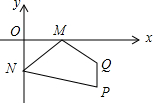如图，点P的坐标是（3，-2），点Q的坐标是（3，-1），点M是x轴上一个动点，点N是y轴上的一个动点，则四边形MNPQ周长的最小值是2$\sqrt{13}$+1．