题目内容
3.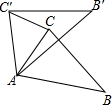 如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 75° |
分析 根据两直线平行,内错角相等可得∠ACC′=∠CAB,根据旋转的性质可得AC=AC′,然后利用等腰三角形两底角相等求∠CAC′,再根据∠CAC′、∠BAB′都是旋转角解答.
解答 解:∵CC′∥AB,
∴∠ACC′=∠CAB=75°,
∵△ABC绕点A旋转得到△AB′C′,
∴AC=AC′,
∴∠CAC′=180°-2∠ACC′=180°-2×75°=30°,
∴∠CAC′=∠BAB′=30°
故选A.
点评 本题考查了旋转的性质,等腰三角形两底角相等的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
14.一只不透明的袋子中装有除颜色外都相同的4个黑球、2个白球,从中任意摸出3个球,下列事件为必然事件的是( )
| A. | 至少有1个球是黑球 | B. | 至少有1个球是白球 | ||
| C. | 至少有2个球是黑球 | D. | 至少有2个球是白球 |
12.在下列二次根式的化简中,被开方数与$\sqrt{2}$的被开方数相同的是( )
| A. | $\sqrt{20}$ | B. | $\sqrt{4}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
 如图,a∥b,∠1=∠2,∠3=40°,则∠4等于70°.
如图,a∥b,∠1=∠2,∠3=40°,则∠4等于70°.