Question

6．如图，矩形ABCD（AD＞AB），AB=1，问BC边上是否存在点M，使得AM⊥DM．

Answer 1

分析 如图，当AD=2，点M是BC中点时，△AMD是直角三角形，由此即可判定．

解答 解：如图，当AD=2，点M是BC中点时，△AMD是直角三角形，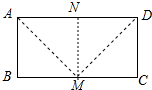

理由：取AD中点N，连接MN．
∵四边形ABCD是矩形，
∴BC=AD，AD∥BC，∠BAD=90°，
∵AN∥BM，AN=BM，
∴四边形ABMN是平行四边形，
∴MN=AB=1，
∵AN=ND=1，
∴MN=NA=ND，
∴△AMD是直角三角形．
由此可知，当AD≥2时，BC边上是否存在点M，使得AM⊥DM，
当AD＜2时，BC边上不存在点M，使得AM⊥DM，

点评 本题考查矩形的性质、直角三角形的判定等知识，解题的关键是判断出AD=2时存在Rt△ADM，题目比较抽象，属于中考常考题型．