题目内容
4.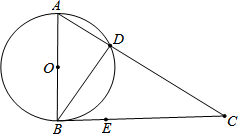 如图:在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E在BC上运动,试探究:当点E运动到何处时,DE与⊙O相切?并证明DE是⊙O的切线.
如图:在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E在BC上运动,试探究:当点E运动到何处时,DE与⊙O相切?并证明DE是⊙O的切线.
分析 若E为BC的中点时,连接OD,DE,如图,根据圆周角定理得∠ADB=90°,由于E为BC的中点,根据直角三角形斜边上的中线性质得DE=BE,则利用等腰三角形的性质有∠BDE=∠DBE,加上∠ODB=∠OBD,则∠BDE+∠ODB=∠DBE+∠OBD,则∠ODE=∠OBD=90°,于是根据切线的判定方法即可判断DE是⊙0的切线.
解答 解:当E为BC的中点时,DE与⊙0相切.
证明如下:连接OD,DE,如图,
∵AB是⊙0直径,
∴∠ADB=90°,
∴∠BDC=90°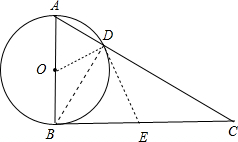 ,
,
又∵E为BC的中点,
∴DE=BE,
∴∠BDE=∠DBE,
∵OB=OD,
∴∠ODB=∠OBD,
∴∠BDE+∠ODB=∠DBE+∠OBD
即∠ODE=∠OBD,
∵∠ABC=90°
∴∠OBD=90°,
∴OD⊥DE
∴DE是⊙0的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列命题中,真命题是( )
| A. | 对角线互相垂直且相等的四边形是正方形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 圆的切线垂直于经过切点的半径 | |
| D. | 平行四边形是轴对称图形也是中心对称图形 |
14.在△ABC中,∠A≤60°,那么△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
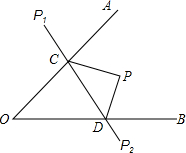 如图所示,P是∠A0B内任一点,以OA、OB为对称轴分别画出点P经轴对称变换后的点P1、P2,连结P1P2,分别与OA、OB相交于点C、D,若P1P2=8cm,求△PCD的周长.
如图所示,P是∠A0B内任一点,以OA、OB为对称轴分别画出点P经轴对称变换后的点P1、P2,连结P1P2,分别与OA、OB相交于点C、D,若P1P2=8cm,求△PCD的周长.