题目内容
14.若点P(m,1)在第二象限内,则点Q(-m,0)在x轴的正半轴上.分析 根据第二象限内点的横坐标小于零,纵坐标大于零,可得不等式组,根据解不等式组,可得答案.
解答 解:由点P(m,1)在第二象限内,得
m<0.
-m>0,
点Q(-m,0)在x轴的正半轴上,
故答案为:x轴的正半轴上.
点评 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
相关题目
5.下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等;
②如果∠1和∠2是对顶角,那么∠1=∠2.
③一个角的余角一定小于这个角的补角.
④三角形的外角大于任何一个内角.
①两条直线被第三条直线所截,内错角相等;
②如果∠1和∠2是对顶角,那么∠1=∠2.
③一个角的余角一定小于这个角的补角.
④三角形的外角大于任何一个内角.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.若$\sqrt{4a+1}$有意义,则a的取值范围为( )
| A. | a≥$\frac{1}{4}$ | B. | a≤$\frac{1}{4}$ | C. | a≥$-\frac{1}{4}$ | D. | a≤$-\frac{1}{4}$ |
3.下列计算正确的是( )
| A. | (2x+3)(2x-3)=2x2-9 | B. | (x+4)(x-4)=x2-4 | ||
| C. | (5+x)(x-6)=x2-30 | D. | (-1+4b)(-1-4b)=1-16b2 |
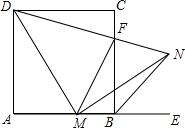 如图,已知正方形ABCD,M是BC边上一点,连DM,作MN⊥DM交∠CBE的平分线于N.
如图,已知正方形ABCD,M是BC边上一点,连DM,作MN⊥DM交∠CBE的平分线于N.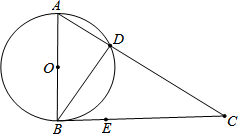 如图:在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E在BC上运动,试探究:当点E运动到何处时,DE与⊙O相切?并证明DE是⊙O的切线.
如图:在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E在BC上运动,试探究:当点E运动到何处时,DE与⊙O相切?并证明DE是⊙O的切线.