题目内容
13.下列命题中,真命题是( )| A. | 对角线互相垂直且相等的四边形是正方形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 圆的切线垂直于经过切点的半径 | |
| D. | 平行四边形是轴对称图形也是中心对称图形 |
分析 根据正方形的判定方法对A进行判断;根据矩形的判定方法对B进行判断;根据切线的性质对C进行判断;根据平行四边形的性质、轴对称和中心对称的定义对D进行判断.
解答 解:A、对角线互相垂直平分且相等的四边形是正方形,所以A选项为假命题;
B、对角线互相平分且相等的四边形为矩形,所以B选项为假命题;
C、圆的切线垂直于经过切点的半径,所以C选项为真命题;
D、平行四边形不是轴对称图形,是中心对称图形,所以D选项为假命题.
故选C.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | (2x+3)(2x-3)=2x2-9 | B. | (x+4)(x-4)=x2-4 | ||
| C. | (5+x)(x-6)=x2-30 | D. | (-1+4b)(-1-4b)=1-16b2 |
1.下列命题错误的是( )
| A. | 四个角相等的四边形是矩形 | B. | 对角线相等的平行四边形是矩形 | ||
| C. | 对角线垂直的四边形是菱形 | D. | 对角线垂直的矩形是正方形 |
8.下列等式成立的是( )
| A. | (-3)-2=-9 | B. | m•m-2•m3=m5 | C. | (-a-1b-3)-2=-a2b6 | D. | (-2m)2÷2m3=$\frac{2}{m}$ |
5.若(a-1)${x}^{{a}^{2}+1}$+bx+c=0是关于x的一元二次方程,则( )
| A. | a=-1 | B. | a≠1 | C. | a=1 | D. | a=±1 |
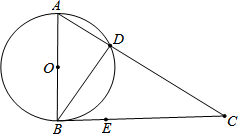 如图:在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E在BC上运动,试探究:当点E运动到何处时,DE与⊙O相切?并证明DE是⊙O的切线.
如图:在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E在BC上运动,试探究:当点E运动到何处时,DE与⊙O相切?并证明DE是⊙O的切线.