题目内容
用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地面:

(1)观察图形,填写下表:
(2)依上推测,第n个图形中黑色瓷砖的块数为 ;黑白两种瓷砖的总块数为 (都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2015块吗?若能,求出是第几个图形;若不能,请说明理由.

(1)观察图形,填写下表:
| 图形 | (1) | (2) | (3) | … |
| 黑色瓷砖的块数 | 4 | 7 | … | |
| 黑白两种瓷砖的总块数 | 15 | 25 | … |
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2015块吗?若能,求出是第几个图形;若不能,请说明理由.
考点:规律型:图形的变化类
专题:
分析:(1)第一个图形有黑色瓷砖4块,黑白两种瓷砖的总块数为15;第二个图形有黑色瓷砖7块,黑白两种瓷砖的总块数为25;第三个图形有黑色瓷砖10块,黑白两种瓷砖的总块数为35;由此填表即可;
(2)由(1)可知每一个图形的黑色瓷砖块数比前一个图形多3,总块数多10,由此求得答案即可;
(3)利用(2)的规律利用“白色瓷砖的块数可能比黑色瓷砖的块数多2015块”联立方程,求得整数解就能,否则不能.
(2)由(1)可知每一个图形的黑色瓷砖块数比前一个图形多3,总块数多10,由此求得答案即可;
(3)利用(2)的规律利用“白色瓷砖的块数可能比黑色瓷砖的块数多2015块”联立方程,求得整数解就能,否则不能.
解答:解:(1)填表如下:
(2)第n个图形中黑色瓷砖的块数为3n+1;黑白两种瓷砖的总块数为10n+5;
(3)能,理由如下:
10n+5-(3n+1)-(3n+1)=2015,
解得:n=503
答:第503个图形.
| 图形 | (1) | (2) | (3) | … |
| 黑色瓷砖的块数 | 4 | 7 | 10 | … |
| 黑白两种瓷砖的总块数 | 15 | 25 | 35 | … |
(3)能,理由如下:
10n+5-(3n+1)-(3n+1)=2015,
解得:n=503
答:第503个图形.
点评:此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
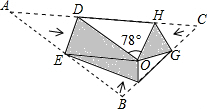 如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )
如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )| A、78° | B、102° |
| C、120° | D、112° |
袋中有4个除颜色外其余都相同的小球,其中1个红色,1个黑色,2个白色.现随机从袋中摸取两个球,则摸出的球都是白色的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在⊙O中,
如图,在⊙O中, |
| AD |
 |
| BC |
| A、70° | B、35° |
| C、60° | D、30° |
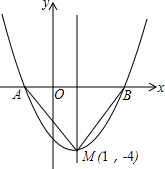 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)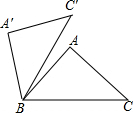 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )