题目内容
8. 如图,AB是⊙O的直径,点E是AB上的一点,过点E作CD⊥AB,交⊙O于点C,D,现有下列结论:①若⊙O的半径是2,点E是OB的中点,则CD=2$\sqrt{3}$;②若CD=2$\sqrt{3}$,点E是OB的中点,则⊙O的半径是2;③若∠CAB=30°,则四边形OCBD是菱形;④若四边形OCBD是菱形,则∠CAB=30°,其中正确结论的序号是( )
如图,AB是⊙O的直径,点E是AB上的一点,过点E作CD⊥AB,交⊙O于点C,D,现有下列结论:①若⊙O的半径是2,点E是OB的中点,则CD=2$\sqrt{3}$;②若CD=2$\sqrt{3}$,点E是OB的中点,则⊙O的半径是2;③若∠CAB=30°,则四边形OCBD是菱形;④若四边形OCBD是菱形,则∠CAB=30°,其中正确结论的序号是( )| A. | ①② | B. | ③④ | C. | ①③④ | D. | ①②③④ |
分析 根据垂径定理和勾股定理即可得到CD=2CE=2$\sqrt{3}$,由CD⊥AB,得到∠CEO=90°,CE=DE=$\frac{1}{2}$CD=$\sqrt{3}$,根据勾股定理即可得到OC=2,根据圆周角定理得到∠COB=60°,推出△COB是等边三角形,得到BC=OC,于是得到OC=OD=BC=BD,根据菱形的判定定理得到四边形OCBD是菱形;根据菱形的性质得到OC=BC,推出OC=OB=BC,得到∠BOC=60°,根据圆周角定理即可得到即可.
解答 解:①∵OC=OB=2,
∵点E是OB的中点,
∴OE=1,
∵CD⊥AB,
∴∠CEO=90°,CD=2CE,
∴CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=$\sqrt{3}$,
∴CD=2CE=2$\sqrt{3}$,故正确;
②∵CD⊥AB,
∴∠CEO=90°,CE=DE=$\frac{1}{2}$CD=$\sqrt{3}$,
∵点E是OB的中点,
∴OE=$\frac{1}{2}$OB=$\frac{1}{2}$OC,
∵OE2+CE2=OC2,
∴($\frac{1}{2}$OC)2+($\sqrt{3}$)2=OC2,
∴OC=2,故②正确;
③∵∠A=30°,
∴∠COB=60°,
∵OC=OB,
∴△COB是等边三角形,
∴BC=OC,
∵CD⊥AB,
∴CE=DE,
∴BC=BD,
∴OC=OD=BC=BD,
∴四边形OCBD是菱形;故③正确;
④∵四边形OCBD是菱形,
∴OC=BC,
∵OC=OB,
∴OC=OB=BC,
∴∠BOC=60°,
∴∠CAB=$\frac{1}{2}∠$BOC=30°,故④正确.
故选D.
点评 本题考查了圆周角定理,垂径定理,菱形的判定和性质,等边三角形的判定和性质,正确的理解题意是解题的关键.

 小学教材全测系列答案
小学教材全测系列答案| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 如图,平面直角坐标系xOy中,抛物线y=ax2(a≠0)经过点B(-2,4).
如图,平面直角坐标系xOy中,抛物线y=ax2(a≠0)经过点B(-2,4).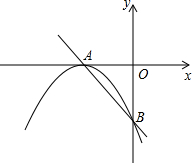 如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B.
如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B.