题目内容
17.在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字-1,-2,1.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)落在函数y=-$\frac{1}{x}$的图象上的概率.
分析 (1)根据题意画树状图即可得到结论;
(2)根据M(x,y)在函数y=-$\frac{1}{x}$的图象上的有(-1,1),于是得到结论.
解答  解:(1)画树状图得,
解:(1)画树状图得,
则点M所有可能的坐标为:(0,-1),(0,-2),(0,1),(1,-1),(1,-2),(1,1),(2,-1),(2,-2),(2,1);
(2)∵M(x,y)在函数y=-$\frac{1}{x}$的图象上的有(-1,1),
∴点M(x,y)落在函数y=-$\frac{1}{x}$的图象上的概率为:$\frac{1}{9}$.
点评 此题主要考查了列表法与树状图法,以及扇形统计图、条形统计图的应用,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )| A. | ($\frac{\sqrt{3}}{2}$)2016 | B. | ($\sqrt{3}$)2016 | C. | 22017 | D. | ($\sqrt{3}$)2017 |
12.已知∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于点B,如图(1),易证BD+AB=$\sqrt{2}$CB,过程如下:
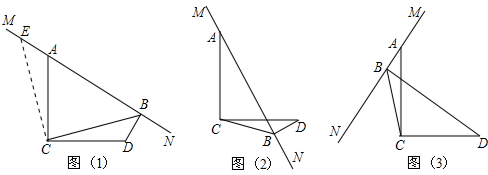
(1)当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(3)给予证明.
(2)MN在绕点A旋转过程中,当∠BCD=30°,BD=$\sqrt{2}$时,则CD=2,CB=$\sqrt{3}$+1.
| 过点C作CE⊥CB于点C,与MN交于点E ∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°, ∴∠BCD=∠ACE. ∵四边形ACDB内角和为360°, ∴∠BDC+∠CAB=180°. ∵∠EAC+∠CAB=180°, ∴BD+AB=$\sqrt{2}$CB. | ∴∠EAC=∠BDC 又∵AC=DC, ∴△ACE≌△DCB, ∴AE=DB,CE=CB, ∴△ECB为等腰直角三角形, ∴BE=$\sqrt{2}$CB. 又∵BE=AE+AB, ∴BE=BD+AB. |

(1)当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(3)给予证明.
(2)MN在绕点A旋转过程中,当∠BCD=30°,BD=$\sqrt{2}$时,则CD=2,CB=$\sqrt{3}$+1.
2.下列运算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | (-3)3=27 | C. | $\sqrt{16}$=4 | D. | $\root{3}{9}$=3 |
9.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{25}$ | B. | $\sqrt{4}$ | C. | $\sqrt{5}$ | D. | $\sqrt{0.8}$ |
 如图,AB是⊙O的直径,点E是AB上的一点,过点E作CD⊥AB,交⊙O于点C,D,现有下列结论:①若⊙O的半径是2,点E是OB的中点,则CD=2$\sqrt{3}$;②若CD=2$\sqrt{3}$,点E是OB的中点,则⊙O的半径是2;③若∠CAB=30°,则四边形OCBD是菱形;④若四边形OCBD是菱形,则∠CAB=30°,其中正确结论的序号是( )
如图,AB是⊙O的直径,点E是AB上的一点,过点E作CD⊥AB,交⊙O于点C,D,现有下列结论:①若⊙O的半径是2,点E是OB的中点,则CD=2$\sqrt{3}$;②若CD=2$\sqrt{3}$,点E是OB的中点,则⊙O的半径是2;③若∠CAB=30°,则四边形OCBD是菱形;④若四边形OCBD是菱形,则∠CAB=30°,其中正确结论的序号是( )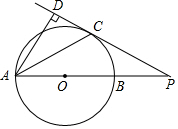 如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB.
如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB.