题目内容
15．
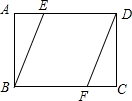如图，矩形ABCD中，E，F分别是AD，BC上两点，且AE=CF．（1）求证：四边形BEDF为平行四边形．
（2）若AB=6，AD=9，则当AE为何值时，四边形BFDE为菱形．
分析 （1）由题意易得ED∥BF，AD=BC而AE=CF，那么可得到ED=BF，即可求证．
（2）结合菱形的四条边相等来求AE的长度．
解答 （1）证明：∵四边形ABCD为矩形，
∴AD∥BC且AD=BC．
又∵AE=CF，
∴AD-AE=BC-CF，即ED=BF，
由ED∥BF且ED=BF，
∴四边形BEDF为平行四边形（一组对边平行且相等的四边形为平行四边形）．
（2）∵四边形BEDF为平行四边形
∴当BE=DE时，四边形BEDF为菱形
设AE=x，则BE=DE=9-x，在直角△ABE中：
x2+62=（9-x）2，
则x=2.5．
∴当AE=2.5时，四边形BEDF为菱形．
点评 本题综合应用了平行四边形的性质和判定，矩形和菱形的判定．要根据条件合理、灵活地选择方法．
练习册系列答案
相关题目
5．平面直角坐标系A、B、C三个坐标分别为（0，0）（0，-5）（-2，2），以这三点为平行四边形的三个顶点，则第四个顶点不可能在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
6．下列各对数中，是二元一次方程3x-y=-7的解的是（ ）
| A． | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$ |
10．方程组$\left\{\begin{array}{l}{x=y+2}\\{x+y=4}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ |