题目内容
20.方程(x+3)(2x-1)=x2-1化成一般形式为x2+3x+2=0,二次项系数是1,一次项系数是3,常数项是2.分析 一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.
在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.
解答 解:把方程(x+3)(2x-1)=x2-1化成一般形式为x2+3x+2=0;这样二次项系数为1,一次项系数为3,常数项为2.
故答案为:x2+3x+2=0,1,3,2.
点评 考查了一元二次方程的一般形式,要确定二次项系数和常数项,首先要把方程化成一般形式.注意在说明二次项系数,一次项系数,常数项时,一定要带上前面的符号.

练习册系列答案
相关题目
10.已知x、y满足方程组$\left\{\begin{array}{l}{x+5y=12}\\{3x-y=4}\end{array}\right.$,则x+y的值为( )
| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
11.下列各组数中,是二元一次方程5x-y=2的一个解的是( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ |
9.下列条件中,不能判定一个四边形是平行四边形的是( )
| A. | 两组对角分别相等 | B. | 两组对边分别相等 | ||
| C. | 一组对边平行且相等 | D. | 一组对边平行,另一组对边相等 |
10.在平行四边形ABCD中,已知AB=4cm,BC=9cm,平行四边形ABCD的面积为18cm2,则∠B 是( )
| A. | 45° | B. | 30° | C. | 60° | D. | 22.5° |
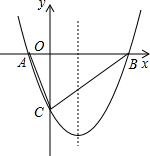 如图,抛物线y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,-2),已知B点坐标为(4,0).
如图,抛物线y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,-2),已知B点坐标为(4,0).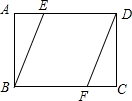 如图,矩形ABCD中,E,F分别是AD,BC上两点,且AE=CF.
如图,矩形ABCD中,E,F分别是AD,BC上两点,且AE=CF. 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8. 如图,AB∥CD,∠1=100°,∠2=120°,则∠a的度数是40°.
如图,AB∥CD,∠1=100°,∠2=120°,则∠a的度数是40°.