题目内容
3.如图1,已知点E在正方形ABCD的边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在图2的AB边上是否存在一点M,使得四边形DMEF是平行四边形?若存在,请给予证明;若不存在,请说明理由.

分析 (1)作辅助线,AG=EC,∠BAE=∠CEF,∠AGE=∠ECF=180°-45°=135°,则△AGE≌△ECF;
(2)①成立,作辅助线,仍然证明△AHE≌△ECF得出结论;
②存在,如图3,过D作DM⊥AE交AB于点M,构成四边形DMEF,证明四边形为平行四边形即可.
解答 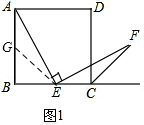 (1)解:如图1,取AB的中点G,连接EG,
(1)解:如图1,取AB的中点G,连接EG,
△AGE与△ECF全等;
(2)①若点E在线段BC上滑动时,AE=EF总成立.
证明:如图2,在AB上截取AH=EC,连接EH,
∵AB=BC,
∴BH=BE,
∴△HBE是等腰直角三角形,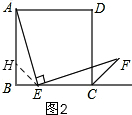
∴∠AHE=180°-45°=135°,
又∵CF平分正方形的外角,
∴∠ECF=135°,
∴∠AHE=∠ECF.
而∠BAE+∠AEB=∠CEF+∠AEB=90°,
∴∠BAE=∠CEF,
∴△AHE≌△ECF,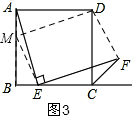
∴AE=EF;
②答:存在,如图3,
过D作DM⊥AE交AB于点M,
则有:DM∥EF,连接ME、DF,
∵在△ADM与△BAE中,$\left\{\begin{array}{l}AD=AB\\∠ADM=∠BAE\\∠BAD=∠ABE\end{array}\right.$,
∴△ADM≌△BAE(AAS),
∴MD=AE,
∵AE=EF,
∴MD=EF,
∵MD∥EF,
∴四边形DMEP为平行四边形.
点评 本题是四边形的综合题,综合考查了平行四边形、正方形、全等三角形的性质和判定,解决此类题的思路为:构造两个三角形全等;熟练掌握正方形的性质是本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
11.下列各组数中,是二元一次方程5x-y=2的一个解的是( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ |
 如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.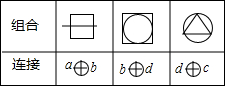 字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形
字母a,b,c,d各代表正方形、线段、正三角形、圆四个图形中的一种,将它们两两组合,并用字母连接表示,如表是三种组合与连接的对应表,由此可推断图形 的连接方式为a⊕c.
的连接方式为a⊕c.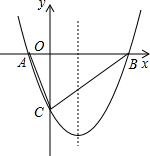 如图,抛物线y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,-2),已知B点坐标为(4,0).
如图,抛物线y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,-2),已知B点坐标为(4,0).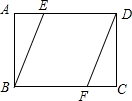 如图,矩形ABCD中,E,F分别是AD,BC上两点,且AE=CF.
如图,矩形ABCD中,E,F分别是AD,BC上两点,且AE=CF. 如图,AB∥CD,∠1=100°,∠2=120°,则∠a的度数是40°.
如图,AB∥CD,∠1=100°,∠2=120°,则∠a的度数是40°.