题目内容
4.解方程(1)$\frac{1}{x-2}=\frac{1-x}{2-x}-3$;
(2)$\frac{6}{x-2}$=$\frac{x}{x+3}$-1.
分析 (1)方程两边同时乘以(x-2)去分母,再解一元一次方程可得x的值,然后再进行检验即可;
(2)方程两边同时乘以(x-2)(x+3)去分母,再解一元一次方程可得x的值,然后再进行检验即可;
解答 解:(1)方程两边同时乘以(x-2)得:
1=x-1-3,
解得:x=5,
检验:把x=5代入x-2≠0,
因此分式方程的解为:x=5;
(2)方程两边同时乘以(x-2)(x+3)得:
6(x+3)=x(x-2)-(x-2)(x+3),
6x+18=x2-2x-x2-x+6,
解得:x=-$\frac{4}{3}$,
检验:把x=-$\frac{4}{3}$代入(x-2)(x+3)≠0,
因此分式方程的解为:x=-$\frac{4}{3}$.
点评 此题主要考查了分式方程的解法,解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.计算3.8×10-7-3.7×10-7,结果用科学记数法表示为( )
| A. | 0.1×10-7 | B. | 1×10-6 | C. | 0.1×10-8 | D. | 1×10-8 |
9.下列条件中,不能判定一个四边形是平行四边形的是( )
| A. | 两组对角分别相等 | B. | 两组对边分别相等 | ||
| C. | 一组对边平行且相等 | D. | 一组对边平行,另一组对边相等 |
16.方程3x-2y=7的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ |
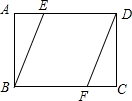 如图,矩形ABCD中,E,F分别是AD,BC上两点,且AE=CF.
如图,矩形ABCD中,E,F分别是AD,BC上两点,且AE=CF. 如图,AB∥CD,∠1=100°,∠2=120°,则∠a的度数是40°.
如图,AB∥CD,∠1=100°,∠2=120°,则∠a的度数是40°.