题目内容

14．不等式组$\left\{\begin{array}{l}{2x+1＜3}\\{4x＞1}\end{array}\right.$的解集是（　　）
A．x＞1B．x＜$\frac{1}{4}$C．$\frac{1}{4}$＜x＜1D．无解

分析 先求出每个不等式的解集，再根据找不等式组解集的规律找出不等式组的解集即可．

解答 解：$\left\{\begin{array}{l}{2x+1＜3①}\\{4x＞1②}\end{array}\right.$
∵解不等式①得：x＜1，
解不等式②得：x＞$\frac{1}{4}$，
∴原不等式组的解集是$\frac{1}{4}$＜x＜1，
故选C．

点评 本题考查了解一元一次不等式组的应用，能根据不等式的解集找出不等式组的解集是解此题的关键．

练习册系列答案
相关题目
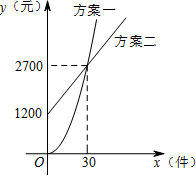4．某公司推销一种产品，公司付给推销员的月报酬有两种方案如图所示：
其中方案一所示图形是顶点在原点的抛物线的一部分，方案二所示的图形是射线．设推销员销售产品的数量为x（件），付给推销员的月报酬为y（元）．
（1）分别求两种方案中y关于x的函数关系式；
（2）当销售量达到多少件时，两种方案的月报酬差额将达到3 800元？
（3）若公司决定改进“方案二”：基本工资1 200元，每销售一件产品再增加报酬m元，当推销员销售量达到40件时，方案二的月报酬不低于方案一的月报酬．求m至少增加多少元？
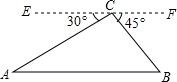5．如图，从热气球C处测得地面A，B两点的俯角分别为30°，45°，此时热气球C处所在位置到地面上点A的距离为400米．求地面上A，B两点间的距离．
2．【课本节选】
反比例函数y=$\frac{k}{x}$（k为常数，k≠0）的图象是双曲线．当k＞0时，双曲线两个分支分别在一、三象限，在每一个象限内，y随x的增大而减小（简称增减性）；反比例函数的图象关于原点对称（简称对称性）．
这些我们熟悉的性质，可以通过说理得到吗？
【尝试说理】
我们首先对反比例函数y=$\frac{k}{x}$（k＞0）的增减性来进行说理．
如图，当x＞0时．
在函数图象上任意取两点A、B，设A（x1，$\frac{k}{{x}_{1}}$），B（x2，$\frac{k}{{x}_{2}}$），
且0＜x1＜x2．
下面只需要比较$\frac{k}{{x}_{1}}$和$\frac{k}{{x}_{2}}$的大小．
$\frac{k}{{x}_{2}}$-$\frac{k}{{x}_{1}}$=$\frac{k（{x}_{1}-{x}_{2}）}{{{x}_{1}x}_{2}}$
∵0＜x1＜x2，∴x1-x2＜0，x1x2＞0，且 k＞0．
∴$\frac{k（{x}_{1}-{x}_{2}）}{{{x}_{1}x}_{2}}$＜0．即$\frac{k}{x_2}$＜$\frac{k}{x_1}$．
这说明：x1＜x2时，$\frac{k}{{x}_{1}}$＞$\frac{k}{{x}_{2}}$．也就是：自变量值增大了，对应的函数值反而变小了．
即：当x＞0时，y随x的增大而减小．同理，当x＜0时，y随x的增大而减小．
（1）试说明：反比例函数y=$\frac{k}{x}$ （k＞0）的图象关于原点对称．
【运用推广】
（2）分别写出二次函数y=ax2 （a＞0，a为常数）的对称性和增减性，并进行说理．
对称性：二次函数y=ax2（a＞0，a为常数）的图象关于y轴成轴对称；
增减性：当x＞0时，y随x增大而增大；当x＜0时，y随x增大而减小．．
说理：①∵在二次函数y=ax2（a＞0，a为常数）的图象上任取一点Q（m，n），于是n=am2．
∴点Q关于y轴的对称点Q1（-m，n）．
而n=a（-m）2，即n=am2．
这说明点Q1也必在在二次函数y=ax2（a＞0，a为常数）的图象上．
∴二次函数y=ax2（a＞0，a为常数）的图象关于y轴成轴对称；
②在二次函数y=ax2（a＞0，a为常数）的图象上任取两点A、B，
设A（m，am2），B（n，an2），且0＜m＜n．
则an2-am2=a（n+m）（n-m），
∵n＞m＞0，
∴n+m＞0，n-m＞0；
∵a＞0，
∴an2-am2=a（n+m）（n-m）＞0，即an2＞am2．
而当m＜n＜0时，n+m＜0，n-m＞0；
∵a＞0，
∴an2-am2=a（n+m）（n-m）＜0．即an2＜am2．
这说明，当x＞0时，y随x增大而增大；当x＜0时，y随x增大而减小；．
【学以致用】
（3）对于函数y=x2+$\frac{2}{x}$ （x＞0），
请你从增减性的角度，请解释为何当x=1时函数取得最小值．
9．圆锥的底面圆半径为2，侧面展开图的面积为12π，则该圆锥侧面展开图的圆心角的度数等于120°．
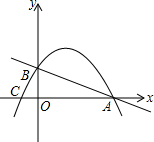19．如图，已知直线y=-$\frac{1}{2}$x+2与x轴、y轴分别相交于A、B两点，过A、B两点的抛物线y=ax2+bx+c交x轴于点C（-1，0）．
（1）求A、B的坐标；
（2）求抛物线的表达式；
（3）抛物线在x轴上方部分是否存在一点P，使得△ACP的面积是△ABO的2倍？如果存在，求出点P的坐标；如果不存在，试求出能使△ACP的面积最大时的点P的坐标．
6．数据1，0，2，3，4的方差是2．
3．若五个数据2，-1，3，x，5的极差为8，则x的值为7或-3．
4．不解方程，判断方程根的情况：
（1）4x2-3x-1=0；
（2）x2-2$\sqrt{2}$x+2=0；
（3）2x2-2x+1=0；
（4）16x2+8x=-3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网