题目内容
1.某商场有甲、乙两箱不同价格的糖果,甲糖果为mkg,单价为a元/kg;乙糖果为nkg,单价为b元/kg.商场决定对两种糖果混合出售,混合单价为$\frac{am+bn}{m+n}$元/kg.(混合单价=$\frac{总价钱}{总质量}$).(1)若a=30,m=30,b=25,n=20,则混合后的糖果单价为28元/kg;
(2)若a=30,商场现在有单价为24元/kg的这种混合糖果100kg,商场想通过增加甲种糖果,把混合后的单价提高15%,问应加入甲种糖果多少千克?
(3)若m=40,n=60,从甲、乙两箱取出相同质量的糖果,将甲箱取出的糖果与乙箱剩余的糖果混合:将乙箱取出的糖果与甲箱剩余的混合,两种混合糖果的混合单价相同,求甲、乙两箱取出多少糖果.
分析 (1)将a=30,m=30,b=25,n=20代入$\frac{am+bn}{m+n}$,计算即可;
(2)设应加入甲种糖果x千克,根据混合后的单价提高15%列出方程,求解即可;
(3)设甲、乙两箱各取出y千克糖果,根据两种混合糖果的混合单价相同列出方程$\frac{by+a(40-y)}{40-y+y}$=$\frac{ay+b(60-y)}{60-y+y}$,整理得出5y(b-a)=120(b-a),进而求出y的值.
解答 解(1)若a=30,m=30,b=25,n=20,
则混合后的糖果单价为$\frac{am+bn}{m+n}$=$\frac{30×30+25×20}{30+20}$=28.
故答案为28;
(2)设应加入甲种糖果x千克,则
$\frac{30x+24×100}{x+100}$=24×(1+15%),
解得:x=150,
经检验,x=150是原方程的解,且符合题意.
答:应加入甲种糖果150千克;
(3)设甲、乙两箱各取出y千克糖果,由题意得
$\frac{by+a(40-y)}{40-y+y}$=$\frac{ay+b(60-y)}{60-y+y}$,
整理得5y(b-a)=120(b-a),
∵两种单价不同的糖果,
∴a≠b,∴b-a≠0,
∴5y=120,
解得y=24,
答:甲、乙两箱糖果各取出24千克的糖果.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目
16.下列关系式中:①y=2x;$②\frac{y}{x}=5$;③y=-$\frac{7}{x}$;④y=5x+1;⑤y=x2-1;⑥y=$\frac{1}{{x}^{2}}$;⑦xy=11,y是x的反比例函数的共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
10.(-1)2015的值是( )
| A. | -1 | B. | 1 | C. | -2015 | D. | 2015 |
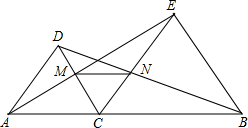 已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N. 如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N=360°或540°或720°.
如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N=360°或540°或720°.