题目内容
6.若x-y=2,x2-y2=4,求x2002+y2002的值.分析 利用平方差公式可得x2-y2=(x+y)(x-y)=4,可以解出x+y的值,得到方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=2}\end{array}\right.$,可以解出x、y的值,然后再把其代入x2002+y2002进行求解.
解答 解:∵x-y=2,x2-y2=4,
∴x2-y2=(x+y)(x-y)=4,
∴x+y=2,
则$\left\{\begin{array}{l}{x+y=2}\\{x-y=2}\end{array}\right.$,
解得x=2,y=0,
∴x2002+y2002=22002.
故x2002+y2002的值是22002.
点评 此题主要考查平方差公式的性质及其应用,解题的关键是解出x、y,是一道基础题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
16.下列计算结果为负数的是( )
| A. | -1+3 | B. | 5-2 | C. | -1×(-2) | D. | -4÷2 |
18.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点P(-1,1),则k的值是( )
| A. | 0 | B. | -2 | C. | 2 | D. | -1 |
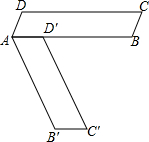 将?ABCD(如图)绕点A旋转后,点D落在边AB上的点D′,点C落到C′,且点C′、B、C在一直线上.如果AB=13,AD=3,那么∠A的余弦值为$\frac{5}{13}$.
将?ABCD(如图)绕点A旋转后,点D落在边AB上的点D′,点C落到C′,且点C′、B、C在一直线上.如果AB=13,AD=3,那么∠A的余弦值为$\frac{5}{13}$.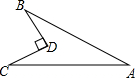 如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.
如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.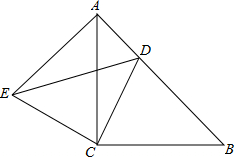 如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.
如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.