题目内容
6.甲、乙两农户是某农业合作社社员,他们今年种植了新型豌豆和土豆,他们生产的农产品由合作社分别以x万元/吨,y万元/吨的价格收购,他们今年种植面积、亩产量与卖出农产品的总收入如下表:| 种植户 | 豌豆 | 土豆 | 卖出两种农产品总收入(万元) | ||
| 种植面积(亩) | 每亩产量(吨) | 种植面积(亩) | 每亩产量(吨) | ||
| 甲 | 4 | 1 | 4 | 3 | 4.8 |
| 乙 | 8 | 1 | 2 | 2.5 | 5.8 |
(2)为了以进一步调动农户的种植热情,合作社计划明年炸收购价不变的情况下对种植这两种农产品给予补贴,补贴标准如下:种植豌豆每亩补贴0.06万元,种植土豆每亩补贴0.05万元,甲种植户计划租30亩地用来种植豌豆和土豆,合作社要求豌豆的种植面积低于土豆的种植面积(两种产品的种植面积均为整数亩),每亩产量均保持不变),为了使甲总收入不低于19.62万元,则他有几种种植方案,并指出哪种种植方案收入最高?
分析 (1)设x万元/吨,y万元/吨的价格收购,根据表格中的等量关系列出方程组求解;
(2)设种植豌豆m亩,则种植土豆面积为(30-m)亩,根据豌豆的种植面积低于土豆的种植面积(两种产品的种植面积均为整数亩),可得m<15,然后分段讨论求解.
解答 解:(1)x万元/吨,y万元/吨的价格收购,
可得:$\left\{\begin{array}{l}{4x+12y=4.8}\\{8x+5y=5.8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=0.6}\\{y=0.2}\end{array}\right.$,
答:x、y的值分别为0.6,0.2;
(2)设种植豌豆m亩,则种植土豆面积为(30-m)亩,
依题意得:m<30-m,
解得:m<15,
使甲总收入不低于19.62万元,
可得:总收入w=0.6m++0.06m+0.2×3(30-m)+0.05(30-m)≥19.62,
解得:m≥12,
∴12≤m<15
综上所述,种植方案有3种,
因为w=0.01m+19.5,所以当m=14时,种植方案收入最高.
点评 本题考查了二元一次方程组的应用及一元一次不等式的应用,解答本题的关键是仔细审题,找到等量关系与不等关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列事件是随机事件的是( )
| A. | 没有水分,种子发芽 | B. | 小张买了一张彩票中500万大奖 | ||
| C. | 抛一枚骰子,正面向上的点数是7 | D. | 367人中至少有2人的生日相同 |
1.一个n边形的内角和比它的外角和至少大120°,则n的最小值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
11.一直角三角形的斜边比一直角边大4,另一直角边长为8,则斜边长为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
18.函数y=$\sqrt{x-3}$中自变量x的取值范围是( )
| A. | x≤3 | B. | x≠3 | C. | x≠-3 | D. | x≥3 |
15.PM2.5是指大气中直径小于或等于0.0000025米的颗粒物.它含有大量有毒有害物质,对人体健康和大气质量的影响很大.用科学记数法表示0.0000025这个数据为( )
| A. | 2.5×10-6 | B. | 25×10-5 | C. | 2.5×106 | D. | 2.5×105 |
16.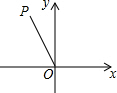 如图,已知∠POx=120°,OP=4,则点P的坐标是( )
如图,已知∠POx=120°,OP=4,则点P的坐标是( )
 如图,已知∠POx=120°,OP=4,则点P的坐标是( )
如图,已知∠POx=120°,OP=4,则点P的坐标是( )| A. | (2,4) | B. | (-2,4) | C. | (-2,2$\sqrt{3}$) | D. | (-2$\sqrt{3}$,2) |
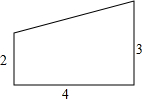 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则能刚好完全覆盖原直角三角形纸片的圆形纸片的半径可能是2$\sqrt{5}$或5.