题目内容
12. 某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.应交电费y(元)与每户家庭用电量x(千瓦时)的函数关系如图所示:
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.应交电费y(元)与每户家庭用电量x(千瓦时)的函数关系如图所示:(1)求出y与x的函数关系式.
(2)小明家5月份交纳电费117元,小明家这个月用电多少千瓦时?
分析 (1)根据图象可知三点坐标(150,74.745),(240,124.092),(330,200.439),可分0<x≤150,150<x≤240,x>240列出函数表达式;
(2)由于小明家5月份交纳电费117元,可知符合150<x≤240的函数关系式,代入y=117即可求出x的值.
解答 解:(1)当0<x≤150时,设y=kx,代入(150,74.745),得:
74.745=150k,
解得:k=0.4983
所以y=0.4983x,
当150<x≤240时,图象过(150,74.745),(240,124.092),设y=kx+b,
$\left\{\begin{array}{l}{150k+b=74.745}\\{240k+b=124.092}\end{array}\right.$,
解得:k=0.5483,b=-7.5
所以y=0.5483x-7.5,
当x>240时,图象过(240,124.092)),(330,200.439),设y=kx+b,
$\left\{\begin{array}{l}{240k+b=124.092}\\{330k+b=200.439}\end{array}\right.$,
解得:k=0.8483,b=-79.5
所以y=0.8483x-79.5
所以y=$\left\{\begin{array}{l}{0.4983x(0<x≤150)}\\{0.5483x-7.5(150<x≤240)}\\{0.8483x-79.5(x>240)}\end{array}\right.$;
(2)把y=117代入y=0.5483x-7.5,得:x=227.065.
小明家5月份交纳电费117元,小明家这个月用电227.065千瓦.
点评 本题主要考查了待定系数法求一次函数关系式,分类讨论是正确解答的关键.

| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
| A. | 7cm | B. | 3cm | C. | 7cm或3cm | D. | 不确定 |
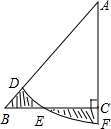 如图,在Rt△ABC中,AC=BC,以A为圆心作$\widehat{DF}$,交AB于点D,交AC的延长线于点F,交BC于点E.若图中两个阴影部分的面积相等,求AC与AF的长度之比(π取3).
如图,在Rt△ABC中,AC=BC,以A为圆心作$\widehat{DF}$,交AB于点D,交AC的延长线于点F,交BC于点E.若图中两个阴影部分的面积相等,求AC与AF的长度之比(π取3).