题目内容
17．
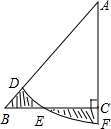如图，在Rt△ABC中，AC=BC，以A为圆心作$\widehat{DF}$，交AB于点D，交AC的延长线于点F，交BC于点E．若图中两个阴影部分的面积相等，求AC与AF的长度之比（π取3）．
分析 若两个阴影部分的面积相等，那么△ABC和扇形ADF的面积就相等，可分别表示出两者的面积，然后列等式即可求出AC与AF的长度之比．
解答 解：∵两个阴影部分的面积相等，
∴S扇形ADF=S△ABC，即：$\frac{45•π•A{F}^{2}}{360}$=$\frac{1}{2}$×AC×BC，
又∵AC=BC，
∴$\frac{AC}{AF}$=$\frac{\sqrt{π}}{2}$=$\frac{\sqrt{3}}{2}$．
点评 此题主要考查了扇形面积的计算方法及等腰直角三角形的性质，能够根据题意得到△ABC和扇形ADF的面积相等，是解决此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某市为了鼓励居民节约用电，采用分段计费的方法按月计算每户家庭的电费．应交电费y（元）与每户家庭用电量x（千瓦时）的函数关系如图所示：
在△ABC中，∠B和∠C的平分线交于点O．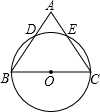
如图所示，△ABC为等边三角形，BC为⊙O的直径，⊙O分别与AB、AC相交于D、E．