题目内容
1．
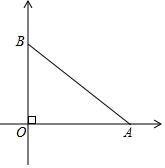甲、乙两位探险者今年到沙漠进行探险，没有了水，需要寻找水源，为了不致于走散，他们用两部对话机联系，已知对话机的有效距离为12千米，早晨8：00甲先出发，他以4千米/时的速度向东行走，1小时后乙出发，他以6千米/时的速度向北行进，上午10：00，甲、乙二人相距多远？还能保持联系吗？
分析 先根据题意得出OA，OB的长，再由勾股定理即可得出结论．
解答 解：∵早晨8：00甲先出发，他以4千米/时的速度向东行走，1小时后乙出发，他以6千米/时的速度向北行进，
∴上午10：00时，OA=8千米，OB=6千米，
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10＜12，
∴甲、乙二人相距10千米，还能保持联系．
点评 本题考查的是勾股定理的应用，熟记勾股定理是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．
如图，在矩形ABCD中，AB=3，∠AOB=60°，则OC的长为（ ）
如图，在矩形ABCD中，AB=3，∠AOB=60°，则OC的长为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
6．
如图是“明清影视城”的一扇圆弧形门，小红到影视城游玩，他了解到这扇门的相关数据：这扇圆弧形门所在的圆与水平地面是相切的，AB=CD=0.25米，BD=1.5米，且AB、CD与水平地面都是垂直的．根据以上数据，请你帮小红计算出这扇圆弧形门的最高点离地面的距离是（ ）
如图是“明清影视城”的一扇圆弧形门，小红到影视城游玩，他了解到这扇门的相关数据：这扇圆弧形门所在的圆与水平地面是相切的，AB=CD=0.25米，BD=1.5米，且AB、CD与水平地面都是垂直的．根据以上数据，请你帮小红计算出这扇圆弧形门的最高点离地面的距离是（ ）| A． | 2米 | B． | 2.5米 | C． | 2.4米 | D． | 2.1米 |
13．正如我们小学学过的圆锥体积公式V=$\frac{1}{3}$πr2h（π表示圆周率，r表示圆锥的底面半径，h表示圆锥的高）一样，许多几何量的计算都要用到π．祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家，创造了当时世界上的最高水平，差不多过了1000年，才有人把π计算得更精确．在辉煌成就的背后，我们来看看祖冲之付出了多少．现在的研究表明，仅仅就计算来讲，他至少要对9位数字反复进行130次以上的各种运算，包括开方在内．即使今天我们用纸笔来算，也绝不是一件轻松的事情，何况那时候没有现在的纸笔，数学计算不是用现在的阿拉伯数字，而是用算筹（小竹棍或小竹片）进行的，这需要怎样的细心和毅力啊！他这种严谨治学的态度，不怕复杂计算的毅力，值得我们学习．
下面我们就来通过计算解决问题：已知圆锥的侧面展开图是个半圆，若该圆锥的体积等于9$\sqrt{3}$π，则这个圆锥的高等于（ ）
下面我们就来通过计算解决问题：已知圆锥的侧面展开图是个半圆，若该圆锥的体积等于9$\sqrt{3}$π，则这个圆锥的高等于（ ）
| A． | $5\sqrt{3}π$ | B． | $5\sqrt{3}$ | C． | $3\sqrt{3}π$ | D． | $3\sqrt{3}$ |
10．下列计算正确的是（ ）
| A． | （-a）6÷a3=a3 | B． | a2•a3=a6 | C． | （2a4）4=16a8 | D． | a+a2=2a3 |
如图，AB为⊙O的直径，D为$\widehat{AC}$的中点，连接OD交弦AC于点F，过点D作DE∥AC，交BA的延长线于点E．