题目内容
6. 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )| A. | 2米 | B. | 2.5米 | C. | 2.4米 | D. | 2.1米 |
分析 连接OF,交AC于点E,设圆O的半径为R米,根据勾股定理列出方程,解方程即可.
解答 解:连接OF,交AC于点E,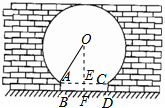
∵BD是⊙O的切线,
∴OF⊥BD,
∵四边形ABDC是矩形,
∴AC∥BD,
∴OE⊥AC,EF=AB,
设圆O的半径为R,在Rt△AOE中,AE=$\frac{AC}{2}$=$\frac{BD}{2}$=0.75米,
OE=R-AB=R-0.25,
∵AE2+OE2=OA2,
∴0.752+(R-0.25)2=R2,
解得R=1.25.
1.25×2=2.5(米).
答:这扇圆弧形门的最高点离地面的距离是2.5米.
故选:B.
点评 本题考查的是垂径定理的应用,掌握平分弦(不是直径)的直径垂直于弦是解题的关键,注意勾股定理的灵活运用.

练习册系列答案
相关题目
16.估计$\sqrt{32}$-$\sqrt{16}$÷2的运算结果在哪两个整数之间( )
| A. | 0和1 | B. | 1和2 | C. | 2和3 | D. | 3和4 |
17.已知关于x,y的方程组$\left\{\begin{array}{l}{3x+2y=p+1}\\{4x+3y=p-1}\end{array}\right.$的解满足x>y,则p的取值范围是( )
| A. | p>-6 | B. | p<-6 | C. | -6<p<5 | D. | p的值无法确定 |
18.下列图形中,由∠1=∠2能得到AB∥CD的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
15.为了解在校学生参加课外兴趣小组活动情况,随机调查了40名学生,结果书法、绘画、舞蹈及其他的频数分别为8、11、12、9,则参加书法兴趣小组的频率是( )
| A. | 0.1 | B. | 0.15 | C. | 0.2 | D. | 0.3 |
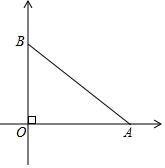 甲、乙两位探险者今年到沙漠进行探险,没有了水,需要寻找水源,为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为12千米,早晨8:00甲先出发,他以4千米/时的速度向东行走,1小时后乙出发,他以6千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
甲、乙两位探险者今年到沙漠进行探险,没有了水,需要寻找水源,为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为12千米,早晨8:00甲先出发,他以4千米/时的速度向东行走,1小时后乙出发,他以6千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?