题目内容
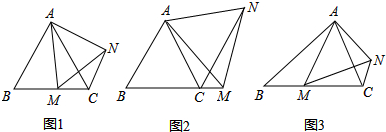
11.【提出问题】(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:BM=CN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论BM=CN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,AB=6,AC=4,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究BM与CN的数量关系,并说明理由.
分析 (1)根据等边三角形的性质可证明△ABM≌△ACN,可证得结论;
(2)方法同(1);
(3)由条件可证明△ABC∽△AMN,再证明△ABM∽△ACN,利用相似三角形的性质可求得结论.
解答 解:
(1)证明:
∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM+∠MAC=∠MAC+∠CAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAM=∠CAN}\\{AM=AN}\end{array}\right.$
∴△ABM≌△ACN(SAS),
∴BM=CN;
(2)成立,理由如下:
∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠CAM=∠CAM+∠MAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAM=∠CAN}\\{AM=AN}\end{array}\right.$
∴△ABM≌△ACN(SAS),
∴BM=CN;
(3)$\frac{BM}{CN}$=$\frac{3}{2}$.
理由如下:
∵AB=BC,AM=MN,
∴$\frac{AB}{AM}$=$\frac{BC}{MN}$,
∵∠AMN=∠ABC,
∴△ABC∽△AMN,
∴$\frac{AB}{AM}$=$\frac{AC}{AN}$,即$\frac{AB}{AC}$=$\frac{AM}{AN}$,
∵∠AMN=∠ABC,
∴∠BAC=∠MAN,
∴∠BAM+∠MAC=∠MAC+∠CAN,
∴∠BAM=∠CAN,
∴△BAM∽△CAN,
∴$\frac{BM}{CN}$=$\frac{AB}{AC}$=$\frac{6}{4}$=$\frac{3}{2}$.
点评 本题为三角形的综合应用,涉及知识点有等边三角形性质、全等三角形的判定和性质、等腰三角形的性质、相似三角形的判定和性质等.在(1)、(2)中证明三角形全等是解题的关键,在(3)中证明三角形相似是解题的关键.本题所考查知识点较为基础,题目难度不大.

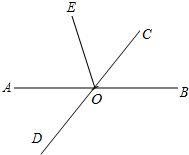 如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |

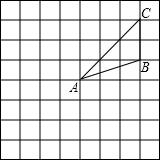 如图所示,在边长为1的网格中,△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.
如图所示,在边长为1的网格中,△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′. 如图,一个直角三角形纸片的锐角顶点A在∠MCN的边OM上移动,移动过程中始终有AB⊥ON于点B,AC⊥OM于点A,∠MON的平分线OP分别交AB,AC于点D、E.
如图,一个直角三角形纸片的锐角顶点A在∠MCN的边OM上移动,移动过程中始终有AB⊥ON于点B,AC⊥OM于点A,∠MON的平分线OP分别交AB,AC于点D、E.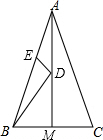 如图,△ABC中,AB=AC=4,∠BAC=45°,AM平分∠BAC,点D、E 分别为AM、AB上的动点,则BD+DE的最小值是2$\sqrt{2}$.
如图,△ABC中,AB=AC=4,∠BAC=45°,AM平分∠BAC,点D、E 分别为AM、AB上的动点,则BD+DE的最小值是2$\sqrt{2}$.