题目内容
3. 如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )| A. | n可以为3和4 | |
| B. | n可以为所有正偶数 | |
| C. | n可以为所有大于2的整数 | |
| D. | 正整数中所有3的倍数的数都可以为n值 |
分析 利用矩形的性质以及正方形的性质,结合勾股定理得出分割方法即可.
解答  解:如图所示:将长为2a、宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,
解:如图所示:将长为2a、宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,
则n可以为:3,4,5,
故n≠2.
故选:B.
点评 此题主要考查了图形的剪拼,正确利用正方形的性质得出分割方法是解题关键.

练习册系列答案
相关题目
12.已知A、B两地相距630千米,在A、B之间有汽车站C站,如图1所示.客车由A地驶向C站、货车由B地驶向A地,两车同时出发,匀速行驶,货车的速度是客车速度的$\frac{3}{4}$.图2是客、货车离C站的路程y1、y2(千米)与行驶时间x(小时)之间的函数关系图象.则下列说法不正确的是( )
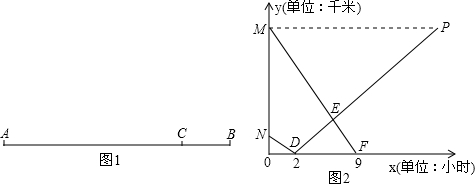

| A. | 货车行驶2小时到达C站 | B. | 货车行驶完全程用时14小时 | ||
| C. | 图2中的点E的坐标是(7,180) | D. | 客车的速度是60千米∕时 |
13.下列计算中,正确的是( )
| A. | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | B. | $\sqrt{8}+\sqrt{2}=\sqrt{10}$ | C. | $\sqrt{8}÷\sqrt{2}=4$ | D. | $\sqrt{8}×\sqrt{2}=4$ |
 如图,线段AB是半径为6的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上(AM<BN),MN=5.若∠MCN=45°,线段AM的长度为3或4.
如图,线段AB是半径为6的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上(AM<BN),MN=5.若∠MCN=45°,线段AM的长度为3或4.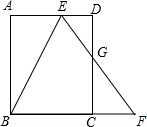 如图,矩形ABCD中,E是AD边上一点,F是BC延长线一点,EF交CD于点G,连接BE.若BE平分∠AEF,G是CD边的中点,tan∠ABE=$\frac{1}{2}$,则$\frac{DE}{AE}$的值为$\frac{3}{4}$.
如图,矩形ABCD中,E是AD边上一点,F是BC延长线一点,EF交CD于点G,连接BE.若BE平分∠AEF,G是CD边的中点,tan∠ABE=$\frac{1}{2}$,则$\frac{DE}{AE}$的值为$\frac{3}{4}$. 如图,四边形ABCD中,连接AC,BD,△ABC是等边三角形,∠ADC=30°,并且AD=4.5,BD=7,5,则CD的长为6.
如图,四边形ABCD中,连接AC,BD,△ABC是等边三角形,∠ADC=30°,并且AD=4.5,BD=7,5,则CD的长为6.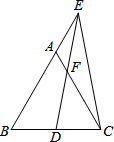 如图,在等边△ABC中,点D是BC中点,点E在BA的延长线上,ED=EC,AC和ED交于点F,若AE=$\frac{12}{5}$,则CF=$\frac{18}{5}$.
如图,在等边△ABC中,点D是BC中点,点E在BA的延长线上,ED=EC,AC和ED交于点F,若AE=$\frac{12}{5}$,则CF=$\frac{18}{5}$.