计算:$\frac{{4y}^{2}{-x}^{2}}{{x}^{3}+{2x}^{2}y+{xy}^{2}}$÷$\frac{x-2y}{{x}^{2}+2xy}$．题目和参考答案——青夏教育精英家教网—

题目内容

1．计算：$\frac{{4y}^{2}{-x}^{2}}{{x}^{3}+{2x}^{2}y+{xy}^{2}}$÷$\frac{x-2y}{{x}^{2}+2xy}$．

分析先将各分式分子、分母因式分解，再将除法转化为乘法，最后约分可得．

解答解：原式=$\frac{（2y+x）（2y-x）}{x（x+y）^{2}}$$÷\frac{x-2y}{x（x+2y）}$
=$\frac{（2y+x）（2y-x）}{x（x+y）^{2}}$×$\frac{x（x+2y）}{x-2y}$
=-$\frac{（x+2y）^{2}}{（x+y）^{2}}$．

点评本题主要考查分式的乘除运算能力，熟练掌握分式运算的顺序是解题的根本和关键．

练习册系列答案

3．当x=2时，分式$\frac{x}{x-2}$没有意义，当x≠-$\frac{1}{3}$时，分式$\frac{2x-1}{3x+1}$有意义．当a=2时，分式$\frac{|a|-2}{a+2}$的值为0．

9．用反证法证明：等腰三角形的底角相等．

16．已知点A，B的坐标分别为（-1，0），（11，0），OB的半径为13，过点A作OB的弦，其中弦长为整数的共有32条．

6．计算：
（1）$\frac{{a}^{2}-4{b}^{2}}{3a{b}^{2}}$•$\frac{ab}{a-2b}$；
（2）$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}+2xy+{y}^{2}}$÷$\frac{x+2y}{{x}^{2}+xy}$．

13．解分式方程：
（1）$\frac{x}{x-3}$=$\frac{x+1}{x-1}$
（2）$\frac{x}{x-2}$-1=$\frac{12}{（x-2）（x+4）}$．

10．

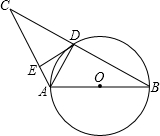如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC于E连接AD，则下列结论正确的个数是（　　）
①AD⊥BC；②∠EDA=∠B；③OA=0.5AC；④DE是⊙O的切线．

11．解分式方程$\frac{4}{x}$-$\frac{1}{x-1}$=1的结果是x=2．

试题分类