题目内容
13.解分式方程:(1)$\frac{x}{x-3}$=$\frac{x+1}{x-1}$
(2)$\frac{x}{x-2}$-1=$\frac{12}{(x-2)(x+4)}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x2-x=x2-2x-3,
解得:x=-3,
经检验x=-3是原方程的根;
(2)去分母得:x2+4x-x2-2x+8=12,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评 此题考查了解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
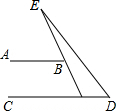 如图所示,AB∥CD,∠ABE=66°,∠D=54°,则∠E的度数为12°.
如图所示,AB∥CD,∠ABE=66°,∠D=54°,则∠E的度数为12°.