题目内容
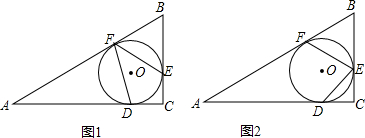
9. 发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B、C、E三点共线,且BC:CE=2:1,连接AE、BD.
发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B、C、E三点共线,且BC:CE=2:1,连接AE、BD.(1)在不添加辅助线和字母的情况下,请在图中找出一对全等三角形(用“≌”表示),并加以证明;
(2)求tan∠BDC的值.
分析 (1)根据SAS证明△BCD与△ACE全等即可;
(2)作AF⊥BE,利用三角函数进行解答即可.
解答 解:(1)△BCD≌△ACE,
∵∠ACB=∠DCE,
∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,
在△BCD与△ACE中$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{DC=EC}\end{array}\right.$,
∴△BCD≌△ACE(SAS);
(2)作AF⊥BE,如图:
∵BC:CE=2:1,
∴设BC=2k,CE=k,
在Rt△AFC中,AC=BC=2k,∠ACF=45°,
∴FC=AC•cos45°=2k×$\frac{\sqrt{2}}{2}=\sqrt{2}k$,EF=FC+CE=$\sqrt{2}$k+k=($\sqrt{2}$+1)k,
∵∠FAC=45°,
∴AF=$\sqrt{2}$k,
由(1)得△BCD≌△ACE,
∴∠BDC=∠AEC,
∴在Rt△AFE中,tan∠BDC=tan∠AEC=$\frac{AF}{FE}=\frac{\sqrt{2}k}{(\sqrt{2}+1)k}=2-\sqrt{2}$.
点评 本题考查了全等三角形的性质和判定,三角函数等知识点的综合运用,题目综合性比较强,有一定的难度,关键是根据SAS证明△BCD与△ACE全等.

练习册系列答案
相关题目
19.将一根圆柱形的空心钢管任意放置,它的主视图不可能是( )
| A. |  | B. |  | C. |  | D. |  |
18.期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是85分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是85分”,上面两位同学的话能反映出的统计量是( )
| A. | 众数和中位数 | B. | 众数和平均数 | C. | 平均数和中位数 | D. | 众数和方差 |
 如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
 如图,在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1=48°.
如图,在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1=48°.