题目内容
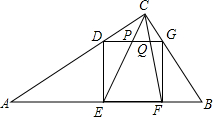 如图,△ABC中,∠C=90°,AC=4,BC=3,正方形DEFG的四个顶点分别在边AC、AB、CB上.
如图,△ABC中,∠C=90°,AC=4,BC=3,正方形DEFG的四个顶点分别在边AC、AB、CB上.(1)求证:△ADE∽△GBF;
(2)求正方形DEFG的边长;
(3)连结CE、CF分别交DG于点P、Q.求证:PQ2=PD•QG.
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:(1)根据同角的余角相等即可证得∠ADE=∠B,然后根据有两个角对应相等的三角形相似即可证得;
(2)设正方形DEFG的边长是x,然后根据△CDG∽△CAB,依据相似三角形的对应边上高的比等于相似比即可求解;
(3)根据△ADE∽△GBF,以及正方形的性质可得EF2=AE•BF,根据相似三角形的性质得到则
=
=
,据此即可证得.
(2)设正方形DEFG的边长是x,然后根据△CDG∽△CAB,依据相似三角形的对应边上高的比等于相似比即可求解;
(3)根据△ADE∽△GBF,以及正方形的性质可得EF2=AE•BF,根据相似三角形的性质得到则
| DP |
| AE |
| QG |
| BF |
| PQ |
| EF |
解答:证明:(1)∵直角△ADE中,∠A+∠ADE=90°,
又∵直角△ABC中,∠A+∠B=90°,
∴∠ADE=∠B,
又∵∠AED=∠GFB,
∴△ADE∽△GBF;
(2)在直角△ABC中,AB=
=
=5,
则AB边上的高是:
=2.4,
∵DG∥AB,
∴△CDG∽△CAB,
∴设正方形DEFG的边长是x,则
=
,
解得:x=
;
(3)∵△ADE∽△GBF,
∴
=
,则DE•GF=AE•BF,
又∵EF=DE=GF,
∴EF2=AE•BF,
∵DP∥AE,
∴△CDP∽△CAE,
∴
=
,
同理,
=
=
,
则
=
=
,
∴
=
,
∴PQ2=PD•QG.
又∵直角△ABC中,∠A+∠B=90°,
∴∠ADE=∠B,
又∵∠AED=∠GFB,
∴△ADE∽△GBF;
(2)在直角△ABC中,AB=
| AC2+BC2 |
| 32+42 |
则AB边上的高是:
| 3×4 |
| 5 |
∵DG∥AB,
∴△CDG∽△CAB,
∴设正方形DEFG的边长是x,则
| x |
| 5 |
| 2.4-x |
| 2.4 |
解得:x=
| 60 |
| 37 |
(3)∵△ADE∽△GBF,
∴
| DE |
| AE |
| BF |
| GF |
又∵EF=DE=GF,
∴EF2=AE•BF,
∵DP∥AE,
∴△CDP∽△CAE,
∴
| CD |
| AC |
| DP |
| AE |
同理,
| CD |
| AC |
| PQ |
| EF |
| QG |
| BF |
则
| DP |
| AE |
| QG |
| BF |
| PQ |
| EF |
∴
| DP•DQ |
| AE•BF |
| PQ•EF |
| EF2 |
∴PQ2=PD•QG.
点评:本题考查了相似三角形的判定与性质以及正方形的性质,是一道综合题目,正确对比例式进行变化是关键,题目难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在Rt△ABC中,∠C=90°,sinB=
,则tanA的值为( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
若一个正多边形的一个外角为60°,则它的内切圆半径与外接圆半径之比是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
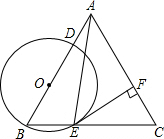 如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.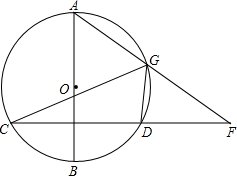 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是
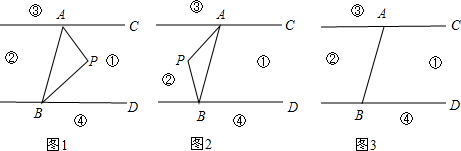
 如图,△ABC的三个顶点坐标分别为A(-4,-2),B(-5,-4),C(0,-4),作一个平移,平面内任意一点P(x0,y0)的像是点P′(x0+7,y0+6),△ABC的像是△A′B′C′,求△A′B′C′的三个顶点A′,B′,C′的坐标.
如图,△ABC的三个顶点坐标分别为A(-4,-2),B(-5,-4),C(0,-4),作一个平移,平面内任意一点P(x0,y0)的像是点P′(x0+7,y0+6),△ABC的像是△A′B′C′,求△A′B′C′的三个顶点A′,B′,C′的坐标. 如图所示,如果?ABCD的一内角∠BAD的平分线交BC于点E,且AE=BE,求?ABCD各内角的度数.
如图所示,如果?ABCD的一内角∠BAD的平分线交BC于点E,且AE=BE,求?ABCD各内角的度数.