题目内容
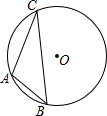 如图,⊙O为△ABC的外接圆,
如图,⊙O为△ABC的外接圆, |
| AC |
 |
| AB |
| ||
| 2 |
考点:圆周角定理,圆心角、弧、弦的关系,解直角三角形
专题:
分析:过点A作AN⊥BC于点N,截取NM=BN,连接AM,求出∠ABC=2∠ACB,AM=CM,根据tan∠ABC=
=
,设AN=
a,BN=2a,求出AM=AB=
a,CM=AM=
a,CN=2a+
a=(2+
)a,解直角三角形即可得出答案.
| ||
| 2 |
| AN |
| BN |
| 2 |
| 6 |
| 6 |
| 6 |
| 6 |
解答:解:过点A作AN⊥BC于点N,截取NM=BN,连接AM,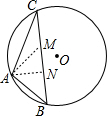
则AM=AB,
所以∠ABC=∠AMB,
∵
=2
,
∴∠ABC=2∠ACB,
∴∠AMB=2∠ACB,
∵∠AMB=∠ACB+∠CAM,
∴∠ACB=∠CAM,
∴AM=CM,
∵tan∠ABC=
=
,
∴设AN=
a,BN=2a,
∴AM=AB=
=
a,CM=AM=
a,
∴CN=2a+
a=(2+
)a,
∴tan∠C=
=
=
-
.

则AM=AB,
所以∠ABC=∠AMB,
∵
 |
| AC |
 |
| AB |
∴∠ABC=2∠ACB,
∴∠AMB=2∠ACB,
∵∠AMB=∠ACB+∠CAM,
∴∠ACB=∠CAM,
∴AM=CM,
∵tan∠ABC=
| ||
| 2 |
| AN |
| BN |
∴设AN=
| 2 |
∴AM=AB=
(
|
| 6 |
| 6 |
∴CN=2a+
| 6 |
| 6 |
∴tan∠C=
| AN |
| CN |
| ||
(2+
|
| 3 |
| 2 |
点评:本题考查了圆周角定理,勾股定理,解直角三角形的应用,解此题的关键是能构造直角三角形,有一定的难度.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
如图①,将量角器与等腰直角△ABC纸片放置成轴对称图形,已知∠ACB=90°,CD⊥AB,垂足为D,半圆(量角器)的圆心与点D重合,测得CE=5cm,将量角器沿DC方向平移2cm,半圆(量角器)恰与△ABC的边AC、BC相切,如图②,则AB的长为( )
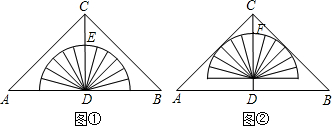

A、8+3
| ||
B、8+6
| ||
C、4+6
| ||
D、16+6
|
在Rt△ABC中,∠C=90°,sinB=
,则tanA的值为( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
在-(-2),|-3|,0,(-1)2,(-2)3这五个数中,正数的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
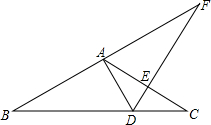 如图,等腰三角形ABC中,AB=AC,点D在BC边上,连接AD,点E在直线
如图,等腰三角形ABC中,AB=AC,点D在BC边上,连接AD,点E在直线 一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.
一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.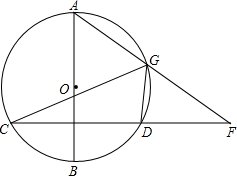 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是