题目内容
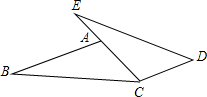 如图,E、A、C三点共线,AB∥CD,∠B=∠E,AC=CD,求证:BC=ED.
如图,E、A、C三点共线,AB∥CD,∠B=∠E,AC=CD,求证:BC=ED.考点:全等三角形的判定与性质
专题:证明题
分析:首先根据平行线的性质可得∠BAC=∠ECD,再利用AAS定理证明△ACB∽△CED,然后再根据全等三角形对应边相等可得结论.
解答:证明:∵AB∥CD,
∴∠BAC=∠ECD,
在△ABC和△CED中
,
∴△ACB∽△CED(AAS),
∴BC=ED.
∴∠BAC=∠ECD,
在△ABC和△CED中
|
∴△ACB∽△CED(AAS),
∴BC=ED.
点评:此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若一个正多边形的一个外角为60°,则它的内切圆半径与外接圆半径之比是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
△ABC中,∠C=90°,AC=1,AB=2,点O是AB的中点,直线l是线段AO的垂直平分线,那么下列命题中,错误的是( )
| A、直线l不经过点C |
| B、点C在直线l上 |
| C、直线l与AC边相交 |
| D、直线l与BC边相交 |
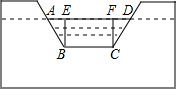 如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m.
如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m. 已知:如图,△ABC和△ADE都是等边三角形.求证:∠ACD=∠ABE.
已知:如图,△ABC和△ADE都是等边三角形.求证:∠ACD=∠ABE.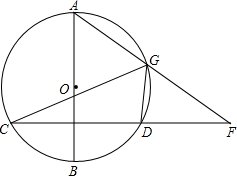 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是